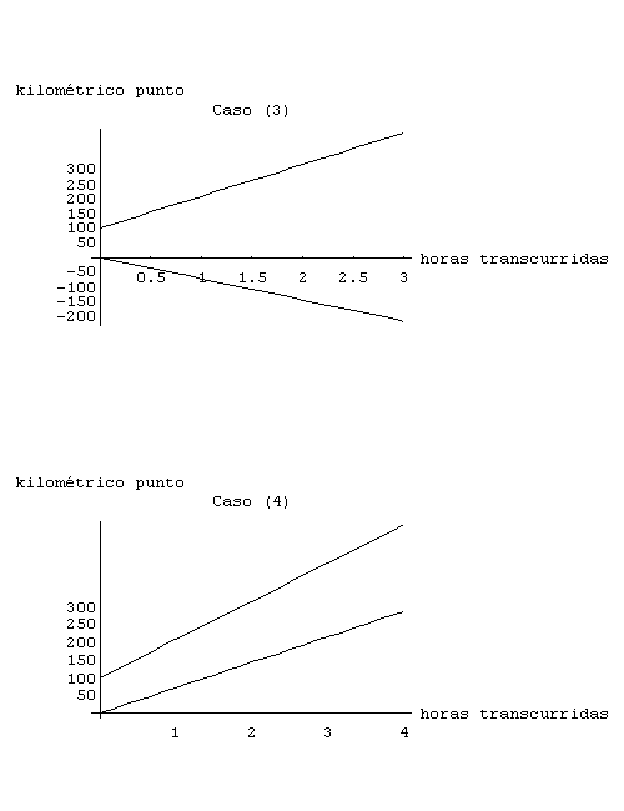Algunos ejemplos de movimiento uniforme

Cuando observamos una tormenta, primero vemos la luz del relámpago y después oímos el estampido del trueno. La razón es que, como es de todos conocido, la luz viaja tan rápido (300,000 Km en un segundo) que a distancias cortas su viaje parece instantáneo de un lugar a otro, mientras que la velocidad del sonido es más bien modesta (340 m/s).

Con un cronómetro en la mano observamos una tormenta. Cuando vemos el primer relámpago encendemos el cronómetro y esperamos a oír el trueno. 4 segundos más tarde oímos el estallido. Cuando el cronómetro indica 12 segundos luce un nuevo relámpago, pero ahora el trueno se oye 5 segundos más tarde, es decir, cuando el cronómetro indica 17 segundos.

De esta información podemos deducir claramente que la tormenta se está alejando de nosotros, puesto que el trueno tardó un segundo más después del segundo relámpago, que del primero. Podemos hacer un esquema de los ocurrido tal y como se indica en la figura 2. Pero podemos obtener muchísima más información de estas medidas tan fáciles de obtener. Cuando vimos el primer rayo, la tormenta se encontraba a 340 m/s × 4 s = 1360 m de distancia, pues el sonido del trueno tardó 4 segundos en llegar hasta nosotros. Cuando cayó el segundo rayo, la tormenta se encontraba a 340 m/s × 5 s = 1700 m, pues ahora el sonido del trueno había tardado 5 segundos. Podemos además deducir la velocidad con la que se aleja la tormenta, pues ésta tuvo que recorrer 640 m (=1700- 1360) en 12 segundos que tardó en verse el segundo rayo después del primero, y por tanto la velocidad es de 640m/12 s ó 53.3 m/s. Esto es, la tormenta recorre 53.3 metros cada segundo, o lo que es lo mismo 192 km/h.

Otro ejemplo instructivo podría ser el siguiente: dos automóviles parten exactamente a las 9:00 de la mañana de dos ciudades situadas a 100 Km con velocidades de 72 km/h y 108 km/h respectivamente. ¿A qué hora se cruzarán?. La cuestión puede parecer un poco confusa; los automóviles ¿parten en la misma dirección?, ¿en direcciones contrarias?... Veamos las diferentes posibilidades en la siguiente figura 3. En los casos (3) y (4) la pregunta carece de sentido, pues los autos no se cruzarán en ningún momento. Analicemos el caso (1). El auto que va a 72 km/h podemos decir que recorre 20 metros cada segundo, y el que se mueve a 108 km/h que avanza 30 metros cada segundo. Por tanto, no es difícil darse cuenta de que transcurrido un segundo, los autos se han acercado 50 metros, es decir, la veinteava parte de un kilómetro. Por tanto, en veinte segundos se acercarán 1 kilómetro, y tendrán que transcurrir 2000 segundos (100×20), ó 33 minutos y 20 segundos para que se crucen ambos automóviles. Problema resuelto.

En caso (2) el planteamiento difiere un poco. Ahora el auto que va a 108 km/h le roba 10 metros cada segundo al que circula a 72 km/h. Por tanto son necesarios 100 segundos para que un auto se acerque un kilómetro al otro, y 10 000 segundo para que el auto más rápido alcance al más lento. Esto es, 2 horas, 46 minutos y 40 segundos.

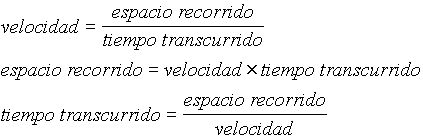
Estos dos ejemplos nos enseñan algunas lecciones interesantes. La primera es que la velocidad de un cuerpo sólo queda bien especificada cuando además del espacio recorrido por unidad de tiempo, damos la dirección en la que se mueve el objeto y el sentido de este movimiento. Esto lo indicamos fácilmente con una flechita, tal y como se hace en las figuras 2 y 3. La segunda es que cuando la velocidad es considerada uniforme, es decir, igual en todo el recorrido, podemos hacer cálculos del espacio recorrido y el tiempo empleado utilizando la siguientes reglas sencillas:

Por últimos podremos aprovechar los anteriores ejemplos para aprender una nueva lección.

4. Representaciones de la posición frente al tiempo.

Ya hemos sido testigos en lecciones anteriores de que a los científicos les gusta inventar algunas artimañas para el estudio de la naturaleza. En el caso del movimiento han creado unas curiosas representaciones del espacio y del tiempo. Utilicemos el ejemplo de los automóviles de la sección anterior para mostrar las ventajas de esta artimaña. Representemos en un eje vertical el tiempo transcurrido desde que parten ambos automóviles de sus respectivas ciudades y en un eje horizontal el punto kilométrico en el que se halla cada automóvil en un determinado instante, para los cuatro casos de la figura 3.

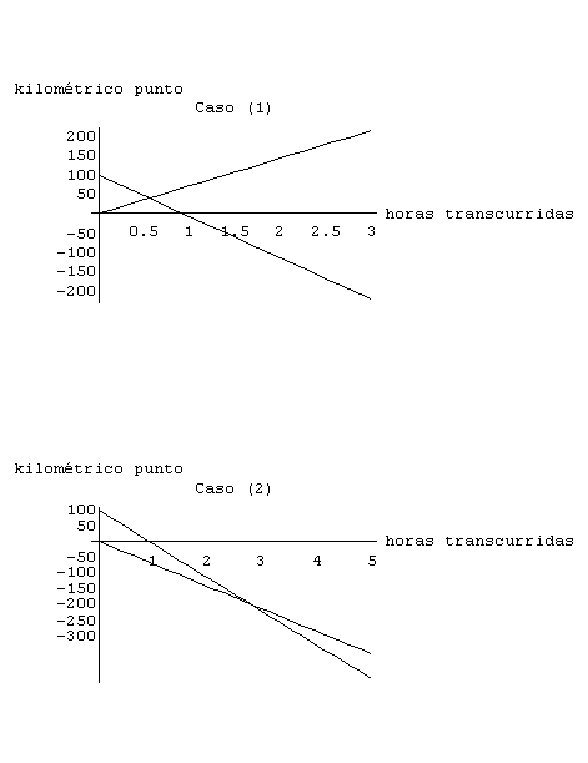
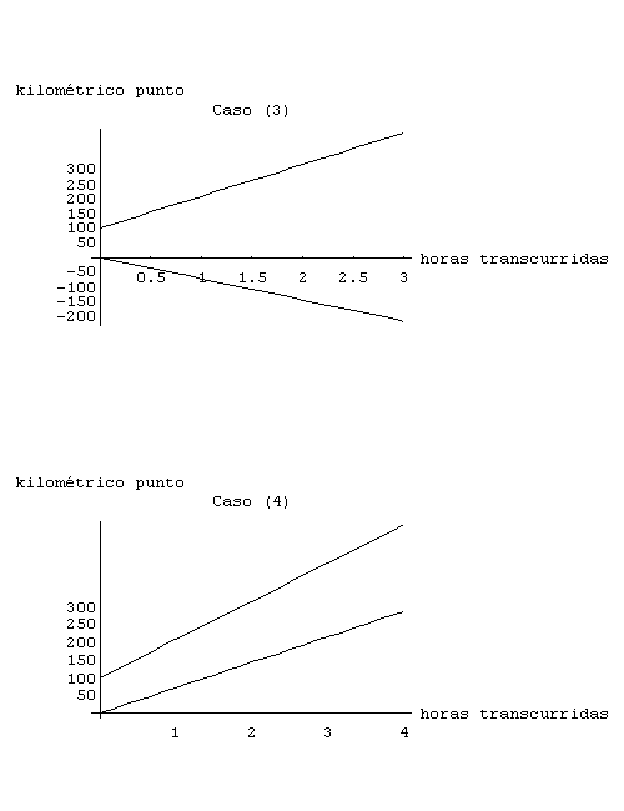
Analicemos en primer lugar la representación gráfica correspondiente al caso (1). Suponemos que la ciudad de la que parte el auto más lento es la más importante, y establecemos allí el punto kilométrico cero. Vemos que el movimiento de éste está representado por una recta de una cierta inclinación que partirá del origen y pasará lógicamente por el kilómetro 72 en una hora. Mientras, el movimiento del auto más rápido viene representado por una recta que, partiendo del kilómetro 100 (donde se encuentra la otra ciudad) pasará por el punto kilométrico -8 en una hora. ¿Qué significa esto del punto kilométrico - 8?. El signo menos lo único que indica en este caso es que nos alejamos de la ciudad más importante en sentido contrario al que tendríamos que tomar para dirigirnos a la ciudad de donde partió el auto más rápido. En el mundo real diríamos que hemos cogido tal carretera en dirección tal ciudad. Se trata simplemente de simplificar el lenguaje de la física...ya ven ustedes.

La observación fundamental en el caso (1) es que las dos rectas coinciden en un punto. Este punto indica el instante y la posición de los dos autos cuando se cruzan. Esto es una información interesante. Cada punto de una representación de este tipo se denomina un suceso. El punto donde se cruzan aquí ambas rectas representa el suceso del cruce de ambos vehículos. Un suceso nos ofrece información sobre la ubicación y el instante de tiempo en el que ocurrió. En este caso vemos que el encuentro ocurrió en el punto kilométrico 40, 33 minutos y 20 segundos después de las 9:00 de la mañana.

En el caso (2) podemos fijarnos que los vehículos también se cruzan. En este caso el suceso ocurre en el punto kilométrico - 200, 2 horas, 46 minutos y 40 segundos después de las 9:00 de la mañana.

En los casos (3) y (4) resulta obvio que los vehículos nunca se cruzan pues las rectas toman direcciones divergentes; no hay punto de corte. La representación del caso (4) nos resulta instructiva, pues nos muestra que el móvil de mayor velocidad es representado por una recta de mayor inclinación; por tanto, parece ser que la inclinación de la recta nos indica la velocidad.

Vamos a utilizar esta artimaña de las representaciones gráficas en el caso de la tormenta del primer ejemplo de la sección anterior. Pero voy a intentar confundir un poquito al lector...¡que ya me estaba empezando a aburrir!. Cambiemos el significado de los ejes: ahora el vertical representa el tiempo transcurrido, y el horizontal la distancia medida desde el observador de la tormenta. Fijémonos en la construcción de la figura 4. A partir de los datos obtenido con el cronómetro podemos obtener toda la información del gráfico. Empecemos situando el suceso de la llegada hasta nuestros oídos del sonido del trueno en la posición del observador a los cuatro segundos.

Podemos entonces trazar una línea recta hasta cortar el eje horizontal (tiempo 0 del cronómetro), de tal forma que cada segundo que nos movamos en la línea del tiempo equivalgan a 340 metros recorridos por el sonido. Así podemos deducir que se produjo el impacto del primer rayo 1360 m a lo lejos. Para averiguar la posición del suceso de la caída del segundo rayo sólo tenemos que prolongar una línea paralela desde los 17 segundos hasta cortar la línea horizontal de 12 segundos de tiempo y ¡voilà!, aparece el suceso de la caída del rayo número dos. Por último, si unimos los dos sucesos de la caída de los rayos obtenemos la línea de movimiento de la tormenta, de la que podemos deducir su velocidad. Sencillo, ¿no?.

Trabajillos y sugerencias.

1 Cuando los primeros astronautas pisaron la Luna colocaron allí un espejo reflector. Si enviamos un haz de luz láser a la Luna, este puede ser reflejado y enviado de vuelta a la Tierra. La experiencia se ha realizado, transcurriendo entre el envío y la recepción del haz láser un periodo de 2,56 segundos exactamente. A partir de este dato, y conociendo que la velocidad de la luz es de unos 300 000 Km/s, calcular la distancia a la que se encontraba la Luna en el momento de hacer la medida. Hacer una representación de la posición frente al tiempo para el movimiento del haz láser.

2 ¿Dónde debe colocarse una persona para oír al mismo tiempo las campanadas de dos campanarios que se encuentran a 3 Km de distancia y que han tocado con 5 segundos de diferencia?. La velocidad del sonido es de 340 m/s.

Representar en una gráfica posición-tiempo el movimiento del sonido de los campanarios.

3 En una carrera de F-1 el coche que va en primera posición entra en los últimos 500 metros a 216 Km/h. Un segundo más tarde lo hace el coche perseguidor a 252 Km/h. Calcular a qué distancia de la meta cogerá el perseguidor la delantera en la carrera.

Representar en una gráfica posición-tiempo el movimiento de ambos autos.

Copyright 1996-2004 Pedro J. Hernández