Métricas en
espacios bidimensionales
Cuando en un espacio Euclídeo bidimensional,
tal y como podría ser una hoja de papel, calculamos la
distancia entre dos puntos de cordenadas cartesianas (x0,
y0) e (x1, y1) utilizando el teorema
de Pitágoras
S212 = (x1
- x0 )2 + (y1 - y0 )2
Que se puede espresar en forma diferencial (en el
límite de puntos muy próximos) como
ds2 = dx2 + dy2
Esta es la distancia euclídea o elemento de
línea del espacio euclídeo. A veces es llamada
métrica, pero la métrica en sentido técnico
es un objeto matemático más abstracto: un tensor.
Por supuesto que la elección de las
coordenadas cartesianas es un hecho arbitrario. Podríamos
haber elegido coordenadas polares (r, q)
de tal manera que el elemento de línea se puede escribir de la
forma
ds 2 = dr 2 + r
2 dq 2
¿Existe alguna manera de reconocer que un
elemento de línea expresado en cualquier tipo de coordenadas
pertenece a un tipo de superficie o espacio particular?. Es decir,
¿existe alguna manera de decidir que los dos elementos
anteriores pertenecen a una hoja de papel (un espacio bidimensional
plano)?. La respuesta es afortunadamente un SÍ. Existe una
función K de las coordenadas conocida como curvatura
gaussiana que se puede calcular a partir del elemento de línea
y que determina la geometría local de la superficie
considerada. En el caso de un espacio euclídeo habitual se
cumple que K = 0, y por eso decimos que es un espacio de curvatura
nula. Nos referimos concretamente a la geometría local,
puesto que, por ejemplo, aunque la superficie de un cilindro sea una
superficie de curvatura nula (K=0) y localmente igual a un plano,
ambos difieren obviamente desde un punto de vista global (o
topológico).
Veamos lo que ocurre en un tipo de superficie
diferente. ¿Cómo podemos, por ejemplo, dar una medida
de longitud entre dos puntos situados sobre una esfera (tal y como
ocurre en nuestro planeta)?. Elijamos las coordenadas usuales de
longitud y latitud (q,j).
Para dos puntos arbitrariamente cerca (q,j)
y
(q
+ dq ,
j + dj )
podemos movernos en latitud a lo largo de un meridiano
una distancia R dq y a
lo largo de un paralelo una distancia R senq
dj hasta
alcanzar el otro punto. La distancia para ir entre los dos puntos
siguiendo el círculo máximo que los une directamente es
entonces
ds2 = R2
dq 2
+ R2 sen2q dj
2
Es el factor sen2q
es el que hace tan
diferente a una esfera de un plano.
Integrando
el elemento de línea ds entre dos puntos separado una
distancia finita, tenemos la longitud de un círculo máximo,
que representa la distancia más corta entre esos dos puntos
(geodésica) en una esfera. En la figura 1 se
pude ver una geodésica que podría representar
perfectamente la trayectoria de un avión que vuela entre dos
ciudades del planeta.
Figura 1.
Este es el elemento de línea de una esfera
en coordenadas esféricas apropiadas. Una manera de representar
una esfera es mediante una proyección sobre un plano, conocida
como proyección estereográfica (ver figura
2.), por razones obvias
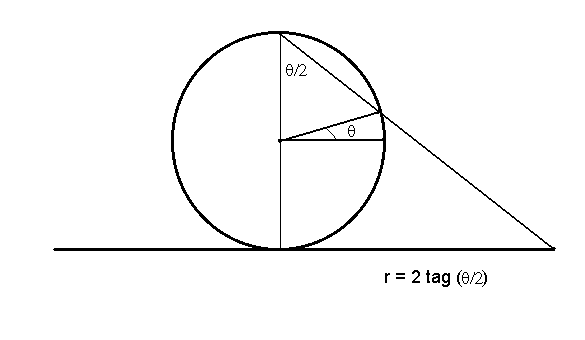 Figura
2.
Figura
2.
La coordenadas (x,y) en el plano proyectado de un
punto de coordenadas esféricas (q,j)
estarán relacionadas de la siguiente manera
x = 2 R tag (q
/2) cosj
y = 2 R tag (q
/2) senj
El elemento de línea de la esfera en estas
coordenadas sería entonces
ds2 = [dx2 +
dy2] [1+ (x2+y2)/4] -2
La proyección estereográfica representa
la superficie finita de una esfera en un mapa plano de dimensiones
infinitas. Tiene la interesante propiedad de no distorsionar las
figuras. Así, círculos en la esfera se convierten en
círculos en el mapa, y no por ejemplo en elipses.
Existen otro tipo de proyecciones muy conocidas en
geografía. Quizás la más famosa es la de
Mercator. La proyección de Mercator es una proyección
cilíndrica modificada para que sea posible que una línea
de rumbo (Sur-Este por ejemplo) sea una línea recta, lo que
facilitaba el trabajo de los marineros al mirar un mapa. Todos
conocemos el efecto de distorsión que produce este tipo de
proyecciones (no nos parece tan obvio por estar tan acostumbrados a
usar mapas en la vida diaria). En la figura 3 se representa a
la izquierda la superficie esférica de la Tierra y a la
derecha una proyección de Mercator de la misma.
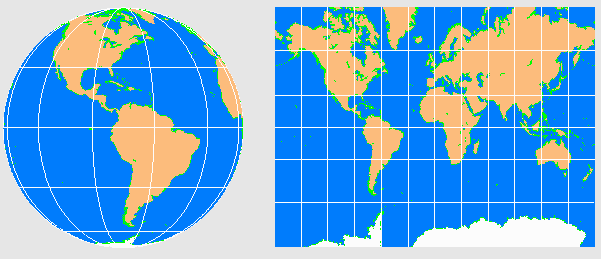
Figura 3.
En un mapa plano de la superficie terrestre las
geodésicas (o círculos máximos) sobre la
superficie terrestre toman la forma que se puede ver en la figura
4 para dos de ellas. Eso significa que por ejemplo un avión
que quisiera viajar entre dos puntos de la superficie terrestre
cubriendo la menor distancia posible debería hacerlo siguiendo
alguna de esas líneas geodésicas, tal y como las rojas
señaladas en la figura 4.

Figura 4.
Existe un tipo de métrica de una variedad más
abstracta de espacio bidimensional que tiene la siguiente forma en
las coordenadas (x,y) anteriores
ds2 = [dx2 +
dy2] [1- (x2+y2)/4] -2
que se diferencia de la de la esfera sólo en
el signo que aparece en el denominador. Esto nos lleva a un posible
generalización del ti po
po
ds2 = [dx2 +
dy2] [1+ k (x2+y2)/4] -2
donde para K = 0 se
reproduce el espacio euclídeo plano, para k = 1 tenemos
la esfera, y para K = -1 el tipo de espacio anteriormente
mencionado. Por razones obvias, el espacio euclídeo se dice un
espacio de curvatura nula, la esfera uno de curvatura positiva y los
espacios del último tipo de curvatura negativa. Un espacio que
se suele poner como ejemplo de espacio de curvatura negativa es una
silla de montar (ver figura 5.).
Figura 5.
 índice
principal de Cosmología
índice
principal de Cosmología
Copyright 1996-2004 Pedro
J. Hernández

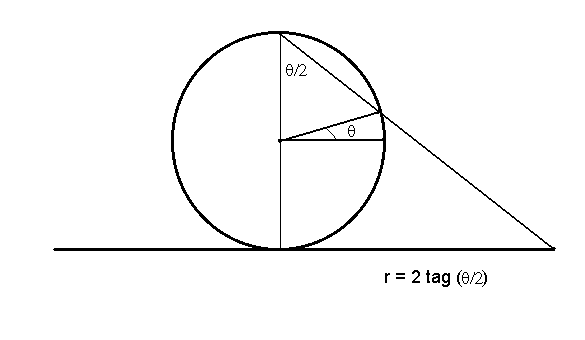 Figura
2.
Figura
2.


 po
po