Milagro I de la gravedad: En cualquier punto interior de una distribución esférica de masa, la fuerza de gravedad neta es la producida por la esfera de masa interior a nuestra posición tal y como si el resto de la masa externa a nuestra posición no existiera.
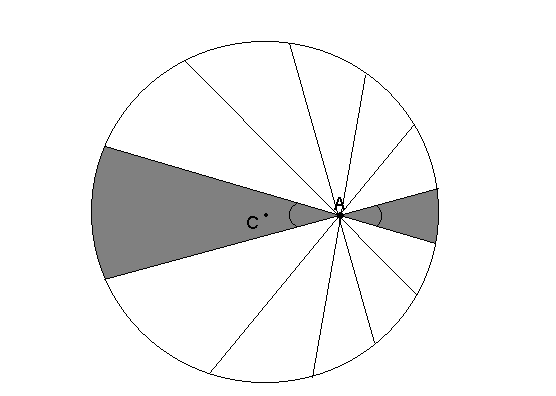
Prueba: Supongamos una distribución continua de masa situada en una cáscara esférica de grosor infinitamente pequeño. Tenemos que demostrar que para cualquier punto del interior de la esfera (tal y como el punto A) la fuerza neta que pruduce la cáscara de masa esférica es cero. Para ello podemos dividir la esfera interior a la capa esférica de materia en secciones tal y como se presentan en la figura 1 (para uno de los planos de corte de la esfera).

Figura 1.
Esta claro (?), que el problema se puede reducir a demostrar que la influencia gravitatoria de cada una de las capas circulares debe estar compensada por la situada en el ángulo opuesto. Este resultado debería ser independiente del número de divisiones, por lo que elijamos para nuestra demostración un número muy grande de divisiones, de tal manera que la sección de superficie incluída en un cono de águlo muy pequeño se pueda aproximar como un círculo donde despreciamos los efectos de curvatura de la esfera (ver figura 2.).
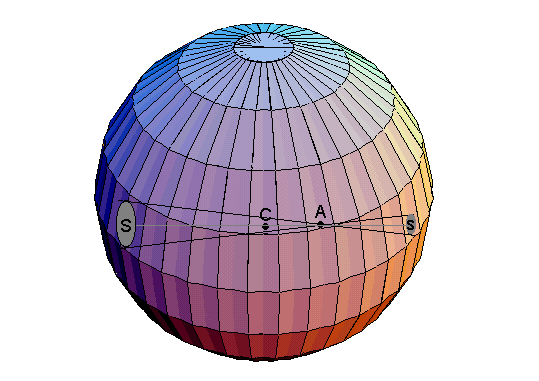
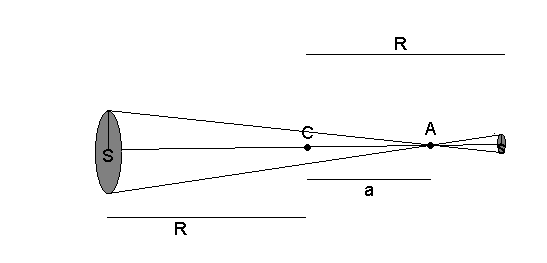
Figura 2.
La cantidad de masa en las secciones de área S y s es proporcional al cuadrado del radio de estas circunferencias. Pero de la figura se deduce que los radios de las superficies S y s están en proporción a las distancias al punto A, y por tanto, las superficies están en proporción al cuadrado de las distancias, y la masa (que es proporcional a la superficie) estará en la misma proporción. Como la fuerza sobre el punto A que ejerce la masa en S y s es proprcional a la masa e inversamente proporcional a la distancia al cuadrado, se sigue inmediatamente que la fuerza que ejercen S y s son idénticas y dirigidas en sentidos opuestos. El resultado puede ser generalizado para una capa esférica de grosor finito si dividimos esta en una cantidad muy grande de capas que puedan ser considera de grosor despreciable (a modo de la disposición de capas en una cebolla), de tal manera que reduzcamos el problema al caso anterior.