Cálculo preciso de órbitas

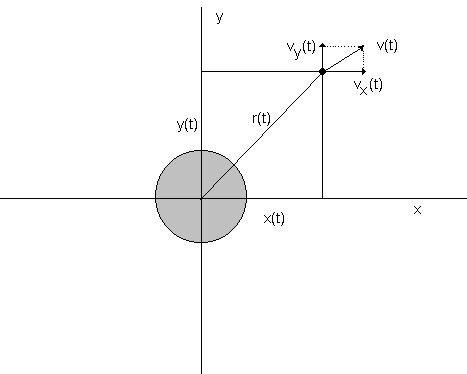
Supongamos que estamos en la base de lanzamiento de la Guayana francesa (muy cerca del ecuador terrestre) y lancemos un cohete con determinada velocidad inicial. Por supuesto, esto no es como un proyectil, pues al principio (gracias a la aceleración de los motores) podemos controlar la velocidad y la dirección. Pero después de un determinado tiempo, la trayectoria de la nave estará determinada principalmente por la velocidad y la dirección que tendrá cuando el cohete ha agotado el combustible y sólo pequeñas correcciones podrán hacerse con los motores auxiliares (ver más detalles sobre órbitas de transferencia). Vamos a escoger la referencia del centro de la Tierra para hacer el cálculo de la posición del cohete y etiquetemos todas las magnitudes según se indica en la figura 26

Figura 26

La ley de gravitación nos dice que la aceleración a la que está sometida la nave está dada por

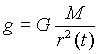
y apunta en dirección hacia el centro de la Tierra. Hagamos una triquiñuela haciendo que el producto G·M sea igual a 1. Eso significa que por ejemplo las distancias que hallemos estarán dadas en megametros (1 millón de metros) y el tiempo en unidades de 50 segundos que denominaremos casiminutos por razones obvias. El cómo han sido elegidas estas unidades lo dejo como ejercicio para el lector interesado. La aceleración podemos descomponerla, en una parte a lo largo de la dirección x y otra parte a lo largo de la dirección y de la siguiente manera:

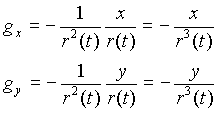
El signo aparece para indicar que esta aceleración está dirigida hacia la izquierda en el primer caso, y hacia abajo en el segundo, pues nuestro convenio va a ser que todo lo que se dirija hacia la derecha y hacia arriba lleva signo positivo. Los factores x/r e y/r aparecen porque la proporción entre las componentes de la aceleración es la misma que la proporción entre los lados del triángulo que tiene por hipotenusa r y por lados x e y. De hecho, en cualquier instante se cumplirá el teorema de Pitágoras aplicado a dicho triángulo:

y lo mismo valdrá para la velocidad y para la aceleración

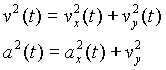
Vamos a intentar calcular una órbita para un satélite que adquiere una velocidad en la dirección horizontal v_x= 0.4 megametros/casiminuto (equivalente a 8 km/s) desde una altura de 1620 km, es decir, que parte de la posición, digamos x = 0, y = 8 megametros (6380+1620 = 8000 km). La aceleración inicial en estas condiciones es

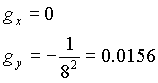
Veamos cómo calculamos lo que ocurre después de digamos 1 casiminuto, y supongamos que durante ese tiempo la aceleración no varía mucho.

Podemos calcular la velocidad media como la velocidad en la mitad del intervalo

v_x (0.5) = v_x(0) + g_x t = 0.4 - 0.0 × 0.5 = 0.4

V_y(0.5) = v_y(0) + g_y t = 0.0 - 0.0156 × 0.5 = -0.078

Y ahora empieza la parte principal de nuestro cálculo:

Utilizando el nuevo valor obtenido para la velocidad media y suponiendo ésta aproximadamente constante, podemos obtener la nueva posición como

x (1) = x(0) + v_x(0.5)· t = 0.0 + 0.4 · 1 = 0.4

y(1) = y(0) + v_y(0.5)· t = 8.0 - 0.0078 · 1 = 7.9922

.........

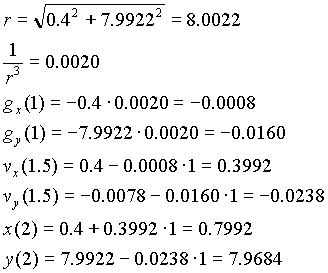
Y así sucesivamente. Por supuesto, hacer algún progreso con una simple calculadora costará algo de tiempo. Pero podemos meter los datos en un ordenador y dejar que éste nos haga el trabajo. Después de 116 pasos obtenemos la mitad de la órbita que podemos ver en la figura 27. El apogeo se encuentra en la posición aproximada y(116) = -14.22 megametros. Por tanto, el periodo aproximado de la órbita es de 232 casiminutos, es decir unas 3 horas y 13 minutos.

Figura 27

Un último comentario sobre la elección del intervalo de tiempo de cada paso en 1 casiminuto. ¿Por qué no 10 o 0.1?. La razón de elegir 1 es que no hay que calcular demasiados pasos y las condición de aceleración casi constante se mantiene de forma aceptable. Si utilizáramos 10, la variación de la aceleración entre dos pasos consecutivos no sería razonable para considerarla constante. Podríamos siempre trabajar con intervalos de tiempo a cada paso menores que 1, pero el esfuerzo no merece la pena, puesto que las condiciones generales de la órbita no van a variar de manera apreciable. Dejo como ejercicio al lector el comprobar que tomando el intervalo de tiempo de 0.1 en 0.1 casisegundos, obtenemos aproximadamente el mismo resultado (consejo: compare los resultados después de 10 pasos con el obtenido en nuestro cálculo de un solo paso).

Hemos utilizado un método denominado de diferencias finitas para calcular la trayectoria continua de una órbita en pasos discretos. Por supuesto, esto en principio se podría hacer de forma analítica utilizando todas las herramientas del cálculo diferencial e integral (ver forma general de la trayectoria). Pero este método tiene muchas ventajas. Primero, es fácilmente implementable en un programa de ordenador. Segundo, podemos variar la expresión de la aceleración a conveniencia, por ejemplo introduciendo la producida por lo cohetes o por cualquier tipo de perturbación (por ejemplo para calcular la influencia de la gravedad Lunar sobre la órbita de nuestro satélite). Tercero, porque es mucho más fácil de entender desde el punto de vista matemático (fíjese el lector que sólo hemos utilizado álgebra elemental.

anterior: Lanzando un satélite artificial

siguiente:La medida de la velocidad de la luz

índice de contenidos