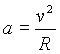
|
siguiente: Cálculo preciso de órbitas |
¿Cómo se las arreglan los ingenieros para lanzar un satélite artificial y ponerlo en la órbita correcta, o para lanzar una nave interplanetaria y que llegue exactamente a la posición donde se encuentra otro cuerpo celeste como Júpiter?. Bueno, el truco consiste en usar la precisión de las leyes de Newton para calcular la trayectoria. Conocer bien una trayectoria implica conocer bien la posición y la velocidad (incluyendo la dirección) en cualquier instante de tiempo. La aceleración puede ser entonces calculada a partir de la ley de Newton y a partir de este conocimiento calcular la nueva posición y las nuevas velocidades en un instante posterior. Vamos a ver los detalles de este cálculo. Pero antes estudiemos cualitativamente el tipo de trayectorias que se pueden obtener. Supongamos para ello que queremos situar un satélite artificial en una órbita perfectamente circular. Ya hemos visto que para mantener un cuerpo en una órbita circular de radio R es necesario que la relación entre la aceleración y la velocidad sea exactamente:
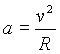
A una distancia R del centro de la Tierra, un cuerpo que gire estará sometido a una aceleración gravitatoria dada por:
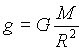
Donde M es la masa de la Tierra. Si igualamos ambas aceleraciones, podemos obtener una relación entre la velocidad y el radio de la órbita dada por:
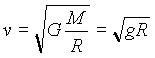
Para un cuerpo en las cercanías de la superficie terrestre, tenemos que g = 9.81 y R = 6380 km, y por tanto esta velocidad es
![]()
que en astronaútica se conoce con el nombre de primera velocidad cósmica, y es la velocidad mínima que hay que imprimir a un cuerpo (despreciando el rozamiento del aire) para que éste no caiga al suelo, sino que vuele alrededor de la tierra (circunferencia C de la figura 24). Si imprimimos al cuerpo una velocidad ligeramente superior a la primera velocidad cósmica, éste empezará a alejarse de la Tierra, pero la gravedad terminará venciendo y lo traerá de nuevo al punto de partida, de tal manera que el objeto describirá una elipse (curvas C1 y C2) con su perigeo en el punto P y con uno de sus focos en el centro de la Tierra. Cuanto mayor es la velocidad inicial del objeto, más alargada es la elipse y más lejos se halla el apogeo de la órbita.

Figura 24
En el caso extremo de llegar a una velocidad denominada segunda velocidad cósmica, el objeto seguirá una trayectoria abierta del tipo C3, que tiene forma parabólica y nunca regresará al punto de partida. Esta velocidad es exactamente
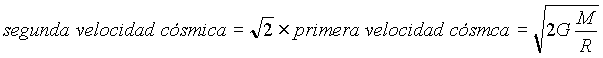
que en el caso de que partamos de las inmediaciones de la superficie terrestre es de aproximadamente 11.2 km/s. A medida que aumentamos la velocidad por encima de la segunda velocidad cósmica la trayectoria es una hipérbola más abierta que se va aproximando a la línea recta X de la figura 24.
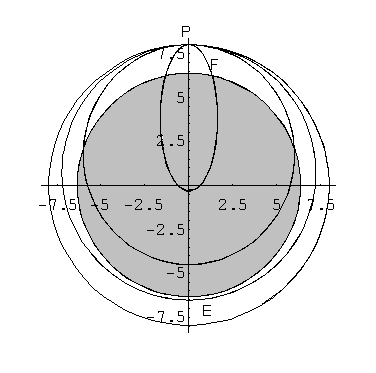
Figura 25
Examinemos ahora lo que ocurriría en el caso de que las velocidades fueran menores que la primera velocidad cósmica. En dicho caso el objeto empezaría a acercarse a la Tierra. Si la velocidad todavía es lo suficientemente grande para que el apogeo de la órbita se encuentre por encima de la superficie terrestre (como es el caso de la elipse E, figura 25), el satélite puede teóricamente mantenerse dando vueltas a la Tierra (despreciando el rozamiento del aire). Pero para velocidades pequeñas el satélite terminará por encontrarse con la superficie terrestre y caer irremediablemente (como es el caso de la órbita F). Esto no sucedería si la Tierra fuera lo suficiente pequeña como para que toda su masa estuviera concentrada en un radio muy pequeño. Como veremos más adelante, esta no es una situación tan ridícula como podría parecer a primera vista. Cuanto menor es la velocidad del satélite en el perigeo, tanto más se acercará el apogeo al centro de la Tierra. Si el objeto está animado con velocidades "terrestres" del orden de unas decenas de metros por segundo, la parte de la elipse que se encuentra por encima de la superficie terrestre es prácticamente indistinguible de una parábola.
Habíamos visto en la sección de lanzamiento de proyectiles que la trayectoria que seguía un proyectil tal y como una bomba que se lanza desde un avión es una parábola. Ahora descubrimos que esto era sólo una aproximación, puesto que habíamos supuesto que la aceleración de la gravedad era siempre vertical. Pero ahora sabemos que esta apunta hacia el centro de la Tierra, y debido a la curvatura de la superficie, su dirección varía de un punto a otro. Cuando lanzamos proyectiles que hacen recorridos modestos, de digamos unos pocos kilómetros como mucho, la aproximación es tan buena como de menos de 3 partes en diez mil. Pero en misiles de largo alcance se pueden recorrer distancia del orden de centenares de kilómetros. Cada 111 km, la aceleración de la gravedad varía aproximadamente 1º en dirección, por lo que hay que considerar la trayectoria como un segmento de elipse y no como una parábola si queremos una buena estimación de lo que realmente ocurre.
|
siguiente: Cálculo preciso de órbitas |
Copyright 1996-2004 Pedro J. Hernández