El concepto de velocidad.

El nuevo auto de Aquiles

Aquiles y Doña Tortuga se dirigen al supermercado en el auto deportivo que se acaba de comprar Aquiles. Doña Tortuga quería probar el nuevo auto y Aquiles ha accedido gentilmente a dejarla conducir. Poco después de salir de casa los para un policía.

Policía: ¡Señora, usted iba a 100 kilómetros por hora!

Doña Tortuga: Eso es imposible, señor, he estado viajando sólo siete minutos. Es ridículo, ¿cómo puedo ir a 100 kilómetros por hora cuando no he viajado una hora?

Policía: ¡Cuénteselo usted al juez!

Aquiles: pero... Doña Tortuga tiene razón. le juro señor policía que sólo hace siete minutos que salimos de casa. Mire, precisamente todavía tengo en la mano la factura del parking.

Policía (poniendo una expresión dudosa):Lo que quiero decir, señora, es esto: si usted siguiera yendo de la misma manera como iba ahora, en la hora siguiente habría recorrido 100 kilómetros.

Doña Tortuga: Bien, mi pie no estaba en el acelerador, y el auto estaba deteniéndose: así que si yo continuara yendo de esa manera no recorrería 100 kilómetros.

Aquiles: Y, en cualquier caso, si siguiera moviéndome de la manera como usted, señor agente,dice que lo estamos haciendo durante una hora más, ¡nos iríamos contra esa pared al final de la calle!

Policía (con ligeros síntomas de impaciencia): Mire, señora, su velocímetro marcaba 100 cuando pasó usted por el control.

Doña Tortuga: precisamente le iba a comentar al señor Aquiles que el velocímetro no está funcionando con propiedad

Aquiles: ¡no me diga usted eso!. ¡Acabo de comprar este coche y ya tiene un fallo!. Voy a demandar a esa empresa. Señor policía, puede usted tomar nota..."25 de julio de..."

Policía: ¡eh!, no empiece con esa...que de la multa no se va a librar.

Doña Tortuga: sí, señor Policía, pero tampoco cambie usted de tema. ¿Qué quiere usted decir con lo de los 100 kilómetros a la hora?

Policía (que ya empezaba a pensar en que todo esto era una tomadura de pelo): Sí, por supuesto, antes de andar una hora usted chocaría esa muralla, pero si anduviera un segundo, recorrería 28 metros; señora, usted iba a 28 metros por segundo y si siguiera andando, el próximo segundo estaría a 28 metros y la muralla está más lejos.

Doña Tortuga: ¡Sí, pero no hay ninguna ley que prohiba ir a 28 metros por segundo!. Hay sólo una ley que prohibe ir a 100 kilómetros por hora.

Policía: Pero... es la misma cosa.

Doña Tortuga: ¿Cómo que es la misma cosa?. Si fuera la misma cosa no habríamos entrado en toda esta discusión acerca de los 28 metros por segundo.

Policía: Mire, está acabando usted con mi paciencia. Ahora mismo me acompañan los dos al juzgado.

Horas más tarde, Doña Tortuga y Aquiles comparecen ante el Juez de Guardia.

Juez de Guardia: ¿qué demonios es toda esa cháchara con lo de los 100 kilómetros por hora, los 28 metros por segundo y demás?. No estoy dispuesto a aguantar toda esta pedantería.

Doña Tortuga: perdóneme usted, señoría, pero el señor policía estaba afirmando que nuestra velocidad era de 28 metros por segundo, y no hay ninguna ley que prohiba ir a esa velocidad.

Juez de Guardia: pero la ley es clara. En la vía donde usted se encontraba no se puede circular a 100 kilómetros por hora, y eso es lo mismo que los 28 metros por segundo.

Doña Tortuga: ¿cómo?

Juez de Guardia: mire, si usted prosiguiera 1/3600 de una hora andando a 100 kilómetros por hora habrá usted recorrido 1/3600 de 100 kilómetros. ¿De acuerdo?.

Doña Tortuga: ¡umm!, déjeme pensarlo un instante... umm... ¡sí, claro!

Juez de Guardia: y eso son aproximadamente 28 metros.

Aquiles (sacando su contador automático de granos de arena): es verdad, Doña Tortuga... ¡mire usted el resultado!.

Doña Tortuga: ahhh... y eso significa que he recorrido 28 metros en 1/3600 de una hora que es precisamente un segundo. ¡28 metros por segundo!.

Juez de Guardia: ¿Por fin ha caído usted en la cuenta?

Doña Tortuga: pero...

Juez de Guardia: sí, ya sé que me va a decir usted que incluso durante ese segundo el coche estaba parando y por tanto que no podría ir a 28 metros por segundo, aún durante ese pequeño intervalo de tiempo.

Doña Tortuga: reconozco que es usted muy agudo, señoría

Juez de Guardia: efectivamente, nuestros agentes están dotados de los últimos medios técnicos. Y con ellos pueden tomar intervalos de tiempo realmente cortos, digamos una millonésima de segundo, y medir la distancia que ha recorrido un auto en ese pequeño instante.

Aquiles: ¿cómo es eso?

Doña Tortuga: si me permite, señoría, lo explicaré yo misma. En una millonésima de segundo, el sofisticado radar del agente le habrá indicado que el coche había recorrido 28 millonésimas de metro, es decir, 28 milésimas de milímetro. Así, que si multiplicamos por un millón ambas cantidades obtenemos los 28 metros por segundo. Y si multiplicamos ésta a su vez por 3600 obtenemos una suma de 100,000 metros recorridos en una hora, lo que nos lleva a los 100 kilómetros por hora de los que hablaba el señor agente.

Juez de Guardia: efectivamente, eso es lo que indica el informe del radar. Así que ahora paguen su multa y váyanse a casa.

Aquiles: ¡pues vaya faena!. Todo esto para terminar pagando la multa.

Doña Tortuga (mientras salen de la sala del juzgado): estimado amigo, mírelo de este modo. Hemos aprendido cómo se mide la velocidad instantánea.

Aquiles: ¿la velocidad qué?

Doña Tortuga: la velocidad instantánea. Fíjese, que no hace falta ir durante mucho tiempo a 100 kilómetro por hora para afirmar que en algún instante podemos llevar esa velocidad. El truco está en escoger una cantidad de tiempo lo más pequeña posible, de tal manera que el auto no se haya movido mucho durante esa pequeña fracción de tiempo. Esa es una idea hermosa y vale el precio que hemos pagado por la multa.

Aquiles: sí, pero ahora conduciré yo... que ya me preocuparé de no alcanzar los 100 kilómetros por hora en ningún instante, por muy pequeño que usted decida elegirlo.

Efectivamente la rapidez media de un cuerpo en movimiento puede ser capturada si se mide como el espacio recorrido por unidad de tiempo. Pongámoslo de una manera clara como (ec.[1])

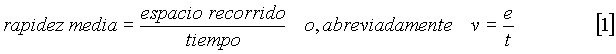
Sin embargo, no está tan claro lo que debemos medir cuando un cuerpo está cambiando de rapidez constantemente, tal y como ocurre con un objeto en caída. Es decir, si un cuerpo se suelta desde una altura de 5 m y tarda del orden de 1 s en caer, ¿ concluimos que el cuerpo se mueve a unos 5 m/s?. Bien, podemos decir que su rapidez media es de unos 5 m/s, pero sabemos que el cuerpo se empieza moviendo muy despacio y acaba moviéndose relativamente más rápido. Entonces, ¿cuál es el truco aquí?. Bueno, lo ideal sería calcular la rapidez en intervalos de tiempo cada vez más chicos, es decir, cada 0,1 s, o cada 0,001 s y así hasta que obtengamos una precisión que nos satisfaga. Pero aquí se nos presenta el problema de que esto es muy difícil de hacer: ¡trate el lector de medir la caída de un objeto en menos de un segundo y verá a lo que me refiero!. No vamos por el buen camino.

Otra posibilidad sería ver qué es lo que pasa cuando tiro un cuerpo desde 10 m de altura. ¿Tardará del orden de 2 s en llegar al suelo?. No, tarda algo menos que 2 segundos, incluso menos de un segundo y medio. La pregunta es inmediata: ¿desde que altura hay que tirar un cuerpo para que tarde 2 s en llegar hasta el suelo?. La respuesta es unos 20 m. Y para que el mismo objeto tarde unos 3 s en caer, hay que tirarlo desde unos 45 m de altura. Podemos observar lo que ocurre en los datos de la tabla 1.

Tabla 1

Si nos fijamos en la rapidez media, la relación con el tiempo es clara. La rapidez media de caída libre es proporcional al tiempo. En otras palabras, si consideramos caídas de objetos que tomen el doble de tiempo, la rapidez media aumenta al doble, si el tiempo es triple, la rapidez media aumentará al triple y así sucesivamente. Esto podemos expresarlo de la siguiente manera (ec.[2])

Webs recomendadas

Física con ordenador

http://www.sc.ehu.es/sbweb/fisica/cinematica/cinematica.htm

Lecturas recomendadas

Richard P. Feyman. FEYNMAN. Vol I. "Mecánica, Radiación y Calor". Sección 8.4: "velocidad".

La forma de presentar el diálogo entre Aquiles, Doña Tortuga y el Policía está inspirada por este capítulo de Feynman. Sin embargo Feynman va un poco más lejos que nosotros y define la velocidad instantánea como velocidad límite o derivada. Los lectores que estén interesados en una difinición precisa del concepto pueden acudir bien a este libro, bien a cualquier libro de texto de física.

Copyright 1996-2004 Pedro J. Hernández