El concepto de aceleración

El número constante g que aparece en la ecuación [2] es lo que se denomina aceleración de la gravedad. La aceleración no es más que la cantidad de cambio de rapidez por unidad de tiempo. ¿Cómo podemos hacer una primera estimación de este número tan importante?. Parece sencillo a primera vista. Si nos fijamos en la tabla 1, podrá parecer que se deduce inmediatamente que la proporción entre el tiempo y la rapidez es de un factor 5, puesto que si multiplicamos el valor del tiempo de caída por 5 obtenemos el valor de la rapidez media. Pero, ¡alto ahí!. Tenemos que ser más cuidadosos. La rapidez media es sólo un valor representativo, puesto que ya hemos señalado que la verdadera rapidez de un cuerpo en caída cambia constantemente, es decir, el verdadero valor de g estará determinado por la rapidez instantánea. Es aquí donde aparece nuestra complicación esencial.

Hagamos una representación gráfica de la rapidez instantánea frente al tiempo. Al ser proporcionales, esto es una línea recta con una cierta inclinación desconocida que está dada precisamente por el valor de la constante g

El truco consiste en darse cuenta que podemos medir el espacio total recorrido si calculamos el producto de la rapidez instantánea para un intervalo de tiempo suficientemente chico y sumamos las contribuciones para cada instante. En la figura 2 están representadas estos productos para pequeños instantes alrededor de cada segundo transcurridos, pero no es difícil darse cuenta que si consideramos todos los instantes cubriremos toda el área del triángulo de la figura.

Calculemos entonces el área de los sucesivos triángulos hasta 1 s, hasta 2 s y así hasta 6 segundos, recordando que la altura del triángulo es la rapidez instantánea que se calcula según la ecuación [2]. Los resultados se muestran en la tabla 2.

Si ahora el lector se molesta en comparar las tablas 1 y 2 verá que si hacemos g = 10, obtenemos los valores deseados para el espacio recorrido.

¿Qué unidades tiene g?. Recordemos que g es una aceleración y se expresa como un cambio de velocidad por unidad de tiempo, es decir m/s cada segundo que habitualmente se expresa como m/s². Por tanto es más correcto poner g = 10 m/s². Es decir, que un cuerpo en caída aumenta aproximadamente de rapidez unos 10 m/s cada segundo de caída transcurrido.

Podemos ahora ir un poco más lejos y hallar una relación general entre el espacio recorrido en la caída y el tiempo de la siguiente manera (ec. [3])

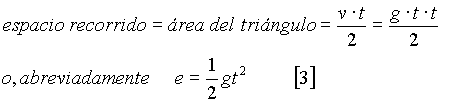
Que se puede representar gráficamente como una parábola, tal y como se puede ver en la figura 3.

Figura 3. Representación del espacio recorrido frente al tiempo en la caída de un cuerpo.

Webs recomendadas

Física con ordenador

http://www.sc.ehu.es/sbweb/fisica/cinematica/cinematica.htm

Lecturas recomendadas

Hewitt, Paul G. FISICA CONCEPTUAL. Segunda Edición. Addison-Wesley Iberoamericana. Capítulo 2.

George Gamov. "Biografía de la física". Alianza Editorial. Sección: "las leyes de la caída". pag 53.

Gamov es un didacta con un sentido del humor ya mítico entre los físicos. Vale la pena leerse no sólo esta pequeña sección sino el libro entero.

Copyright 1996-2004 Pedro J. Hernández