Características básicas de la gravedad

Todos los objetos parecer querer caer hacia el centro de la Tierra. Coja el lector un cordel del que cuelgue un peso, y la dirección que marca el hilo (conocida como dirección de la plomada) es muy aproximadamente la dirección del centro de la Tierra. Pero ¿qué tiene el centro de la Tierra que le hace un lugar tan especial que todos los cuerpos quieran reunirse allá abajo?. La respuesta es que no hay nada de especial. Veamos lo que ocurre simplificando un poco la estructura de la Tierra. Supongamos que tenemos un conjunto de objetos situados de tal manera que formen una circunferencia, tal y como se indica en la figura 9. Es obvio que los objetos situados simétricamente a ambos lados del objeto que cae hacia nuestra Tierra simplificada tiran de la misma manera, con lo que el resultado es que el cuerpo se mueve en la dirección que precisamente se dirige hacia el centro.

Figura 9. Dirección de atracción que experimenta un cuerpo debida una distribución circular de masas.

Es decir, que de la suposición de que todos los cuerpos están sometidos a la acción de la gravedad deducimos fácilmente una propiedad de la dirección de caída de los cuerpos. Por tanto es una idea hermosa suponer que esto es cierto y que la gravedad es una fuerza universalmente válida para cualesquiera dos cuerpos que consideremos.

Veamos qué ocurre con objetos más alejado de la Tierra. El objeto lejano más próximo a la Tierra es la Luna. ¿Está cayendo la Luna hacia la Tierra?. Si la atracción de la gravedad es tan universal como habíamos supuesto, esto tiene que ser así. Pero nosotros no vemos que la Luna se caiga sobre nosotros. Veamos cuál es el truco de la Luna. Pensemos por ejemplo en un proyectil que es lanzado horizontalmente desde un avión. ¿Existe alguna manera de que este proyectil nunca alcance el suelo?. Recuerde el lector que un cuerpo cae aproximadamente 5 metros en el primer segundo de caída. ¿Qué ocurriría si en ese segundo el cuerpo se haya movido de tal manera que la superficie de la tierra haya bajado justo esos 5 metros?. Ese es el truco para nunca caerse a la Tierra. Si nos fijamos en la figura 10, podemos obtener la velocidad necesaria para que ocurra esto

Figura 10

Del triángulo de la figura y aplicando el teorema de Pitágoras obtenemos (ec.[7]):

donde R es el radio de la tierra, unos 6300 Km. Sustituyendo esta cantidad en la ecuación anterior obtenemos unos 7945 m/s (28,600 km/h). En definitiva, tenemos que un objeto que se moviera horizontalmente con una velocidad de 28,600 km/h en las cercanías de la superficie terrestre no caería, sino que terminaría viajando en círculo alrededor de la Tierra. Bien, ese es el truco que emplea la Luna para no caerse sobre la Tierra. ¿Cómo podemos calcular la velocidad de la Luna?. Bien, no es difícil siempre que conozcamos la distancia a la Luna y el tiempo que tarda en dar una vuelta. La distancia a la Luna es de unos 384.000 km y su periodo de traslación alrededor de la Tierra es de unos 29 días. Por tanto, la velocidad de la Luna la podemos estimar como:

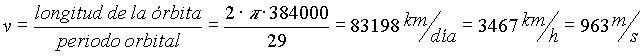
Ésta es nuestra primera indicación de que la Luna está sometida a una fuerza de gravedad menor que la de un objeto en las cercanías de la superficie terrestre. Veamos cuántos metros cae la Luna en un segundo utilizando la ec. [7] donde cambiamos R por la distancia Tierra-Luna, la velocidad por la de la Luna y los 5 metros que cae un cuerpo en el primer segundo sobre la superficie terrestre por una distancia x desconocida que cae la Luna en 1 segundo:

Por lo que la relación entre las aceleraciones de la gravedad en la superficie terrestre y a la distancia de la Luna es de aproximadamente

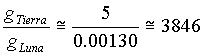
Es decir, la gravedad en la superficie terrestre parece ser una 3846 veces mayor que a la distancia de la Luna. Teniendo en cuenta que la Luna está unas 61 veces más lejos del centro de la Tierra que la superficie terrestre, esto nos lleva a sospechar que la gravedad debe disminuir como el cuadrado de la distancia puesto que 61² = 3721, que se acerca a 3846 en algo más del 3%, un error bastante pequeño si consideramos que nuestra estimación ha sido bastante grosera. Este fue uno de los test que empleó Newton para su ley del inverso del cuadrado de la distancia.

Copyright 1996-2004 Pedro J. Hernández