¿Cómo se han estimado las distancias?

En la sección anterior hemos utilizado una serie de números como el radio terrestre, la distancia a la Luna y el periodo de traslación de ésta alrededor de la Tierra. ¿Cómo se han obtenido estos números?.

La primera estimación precisa del tamaño de la Tierra la hizo el gran geógrafo de la antigüedad Eratóstenes (276?-195? a..C.). Eratóstenes había oído relatos de viajeros que decían que a mediodía del 21 de junio el sol no arrojaba sombra en un manantial de Syene (la moderna Assuán), y que por consiguiente su luz caía perpendicularmente sobre las cabezas de los observadores. Él, por su parte, sabía que en Alejandría (donde residía) el sol siempre arrojaba sombra. Por los datos que tenía consideró que Syene estaba justo al sur de Alejandría. Se le ocurrió entonces que si podía medir la longitud de la sombra del sol en Alejandría a la hora en que no había sombra en Syene, podría calcular la circunferencia de la Tierra. El 21 de junio Eratóstenes midió la sombra de un obelisco de Alejandría y mediante simple geometría calculo que la sombra proyectada correspondía a una desviación de los rayos solares respecto a la vertical de 7º 14'. Esto corresponde a 1/50 de la circunferencia total de la Tierra (360º). La circunferencia de la Tierra era por tanto igual a 50 veces la distancia que mediaba entre Syene y Alejandría. Pero, ¿Cuál era esa distancia?. Él sabía, por los viajeros, que los camellos necesitaban unos 50 días para cubrirla, y que un camello recorría cien estadios en un día. La distancia entre Syene y Alejandría era por la tanto de cinco mil estadios (50×100). Eratóstenes calculó por tanto que la circunferencia de la Tierra era de doscientos cincuenta mil estadios (50×5000). No estamos seguros de cuál es el equivalente exacto entre los estadios y los metros, pero los mejores cálculos otorgan unos 185 metros de largo. El "estadio griego", del cual proviene nuestra palabra estadio, era una carrera pedestre que tenía precisamente esa longitud. Según estos cálculos, Eratóstenes llegó a la conclusión de que la circunferencia terrestre medía unos 46.190 kilómetro, cifra que sobrepasa a la medida actual en un 15%, pero la esta estimación fue la más precisa que se ha hecho hasta los tiempos modernos.

¿Cómo se puede calcular la distancia que nos separa de la Luna?. Bien, el truco es similar al que empleó Eratóstenes. Tenemos que averiguar por ejemplo en qué lugar de la Tierra la Luna está saliendo por el horizonte y en qué lugar se haya justo sobre nuestras cabezas. La situación queda representada en la figura 11.

Figura 11

El triángulo formado por el centro de la Tierra, el lugar donde la Luna es vista en el horizonte y la propia Luna es rectángulo. Conocemos el radio de la Tierra y podemos estimar el ángulo a que es de 89.05º. Por simple trigonometría tenemos que:

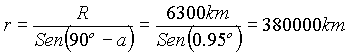
Por supuesto que los cálculos anteriores son una artimaña para que la cosa sea sencilla. Resulta obviamente más sencillo de medir si elegimos dos puntos arbitrarios sobre la Tierra a lo largo del mismo meridiano aproximadamente y medimos la diferencia de ángulos de la Luna con respecto a la vertical. Pero en este caso el cálculo trigonométrico es un poco más complejo. Como siempre, queda como ejercicio para los lectores con más conocimientos matemáticos.

Una vez conocida la distancia que nos separa de la Luna, resulta bastante sencillo dar una estimación de sus dimensiones. El diámetro aparente de la Luna es de aproximadamente medio grado. Por tanto, su radio se puede calcular como:

Una estimación más precisa nos llevaría a unos 1738 km, pero nuestro error del 4.5% es una medida bastante aceptable.

Por último, el tiempo que tarda la Luna en dar una vuelta alrededor de la Tierra puede ser estimado a partir de la repetición de las fases lunares. Este fenómeno se produce cada aproximadamente 29 días, aunque varía en cada mes lunar, del que deriva nuestro mes del calendario.

Figura 12. Explicación de las fases lunares (ver animación)

Copyright 1996-2004 Pedro J. Hernández