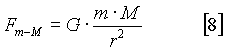
|
anterior: ¿Cómo se ha estimado las distancias? |
siguiente:Pesando la Tierra |
Isaac Newton (1642-1727) se basó en las consideraciones hechas en las secciones precedentes para establecer la ley que caracterizaba a la gravedad de la siguiente manera (ec.[8]):
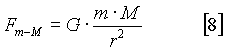
Siendo Fm-M la fuerza de gravedad con la que se atraen dos masas de magnitud M y m; r la distancia entre los centros de las masas y G una constante que tenemos que medir. Ya habíamos indicado cómo llegamos a la sospecha de que la fuerza debería disminuir con el cuadrado de la distancia. El producto de las masas M y m, que aparece en el numerador de la expresión [8] parece lógico por dos razones:
las masas mayores producirán gravedades de mayor magnitud y la manera más sencilla de hacerlo sería que este aumento sea proporcional
el hecho de poner las dos masas de esa forma garantiza que la fuerza de atracción sea igual desde el punto de vista de ambas masas, es decir, la fuerza con que la masa M atrae a la masa m es exactamente la misma que la fuerza que produce m sobre M. (Principio de acción y reacción)
El siguiente paso es cómo caracterizar el movimiento de un objeto cuando está sometido a una fuerza del tipo dado en la expresión [8]. Para ello Newton ensayó la siguiente ley general (ec.[9])
|
F = m a |
[9] |
Que nos dice que una fuerza de magnitud F produce en un objeto de masa m una aceleración de magnitud a dirigida en la misma dirección de la fuerza. Esta fue la intuición fundamental de Newton. Es una ley muy sencilla, pero veremos lo potente que resulta como descripción de los movimientos de cualquier objeto sometidos a una fuerza.
Empecemos sustituyendo la expresión para la fuerza de gravedad [8] en la nueva ley del movimiento [9],
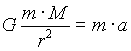
que puede representar la aceleración a la que está sometido un cuerpo de masa m situado a una distancia r de un cuerpo de masa M. El cuerpo de masa M podría ser perfectamente la Tierra. Vemos que la masa m del objeto que está cayendo sobre la Tierra puede ser eliminada de ambos miembros de la ecuación. Es decir, que la aceleración de la gravedad es independiente de la masa de los cuerpos que caen, un hecho que ya habíamos observado anteriormente. Por tanto, la aceleración de la gravedad alrededor de un cuerpo de masa M puede ser obtenida como,
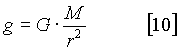
La expresión [10] nos da una relación entre la aceleración de la gravedad, el radio de la Tierra y la masa de la Tierra. Como ya tenemos una estimación de la aceleración de la gravedad de 10 m/s2 y una del radio de la Tierra de unos 6400 km, podríamos pesar la Tierra si conociéramos la constante G.
El lector debería notar que Newton hizo un supuesto de especial importancia al suponer que la masa gravitatoria de un cuerpo que se introduce en la ley de Gravitación [8] tiene el mismo valor numérico que la masa inercial que se introduce en la ley del movimiento [9]. No hay ninguna razón fundamental para que esto tuviese que ser así, aunque es lo más sencillo y funciona, pues nos lleva a la observación de Galileo de que todos los cuerpos caen con la misma aceleración independientemente de sus masas.
|
anterior: ¿Cómo se ha estimado las distancias? |
siguiente:Pesando la Tierra |
Copyright 1996-2004 Pedro J. Hernández