Cavendish midió la fuerza directa entre dos grandes bolas fijas de plomo y dos bolas más pequeñas de plomo en los extremos de un brazo suspendido de una fibra muy fina, conocida como fibra de torsión.
figura 13
|
anterior: Ley de gravitación universal y leyes del movimiento |
siguiente: El movimiento de la Tierra |
El primer hombre que midió la fuerza de la gravedad con masas situadas en un laboratorio fue Henry Cavendish (1731-1810) utilizando un aparato como el esquematizado en la figura 13.
|
Cavendish midió la fuerza directa entre dos grandes bolas fijas de plomo y dos bolas más pequeñas de plomo en los extremos de un brazo suspendido de una fibra muy fina, conocida como fibra de torsión. |
figura 13 |
Midiendo cuánto se tuerce la fibra se puede estimar la magnitud de la fuerza, verificar que depende del cuadrado de la distancia y determinar su intensidad. De las medidas de Cavendish se dedujo que la constante G debe valer 6.67·10-11 si las masas se expresan en kg y las distancias en metros.
Bueno, si sustituimos ahora en la expresión [10], podemos hallar la masa de la Tierra como
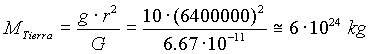
¿Y si nuestra ley estuviera completamente equivocada?. Veamos si la masa de la Tierra obtenida tiene un valor razonable. Vamos al calcular la densidad media del planeta dividiendo esta masa por el volumen de la esfera terrestre,
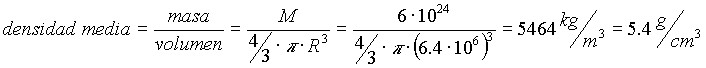
lo que significa que cada cm3 del material terrestre debe de pesar, en término medio, unos 5.4 g. 1 cm3 de agua pesa aproximadamente 1 gramo y 1 cm3 de hierro, unos 7.9 g, con lo que nuestra estimación está en algún lugar intermedio entre las densidades del agua y del hierro, lo que significa que el valor que hemos obtenido para la masa de la Tierra es al menos consistente con la de los materiales que la componen, un dato para el optimismo.
|
Figura 14 |
Por último me gustaría enseñar al lector un método más preciso para medir la aceleración de la gravedad. Se trata de utilizar un péndulo, es decir, un peso atado a un cordel. Se puede observar en la figura 14, que la aceleración que va en la dirección del movimiento de la masa viene dada como ga = g · sen a. Si el ángulo a es pequeño, el seno del ángulo puede sustituirse aproximadamente por el ángulo expresado en radianes. Si además tenemos en cuenta que el arco de circunferencia que barre el peso es s = l · a, donde l es la longitud del cordel, nos queda en definitiva que:
|
Cuando tengamos una expresión donde la aceleración del movimiento es proporcional al espacio recorrido, estamos ante un movimiento de tipo oscilatorio (como el del péndulo) con un periodo (o tiempo en el que tarda en ir y volver) dado por
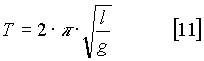
Por tanto, si hacemos algunas medidas con un péndulo, y calculamos el tiempo de ida y vuelta, podremos hacer una estimación de la aceleración de la gravedad como:
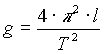
de donde se puede obtener un valor tan preciso como 9.81 m/s2 para la aceleración de la gravedad. Sustituyendo este valor en nuestra estimación de la masa de la Tierra obtenemos 5.98·1024 kg. (más detalles pulsar aquí)
Para aquel lector que se le haya escapado el razonamiento anterior, le propondré una técnica algo chapucera pero a veces efectiva que se conoce como "análisis dimensional". Obviamente, las tres magnitudes físicas que pueden influir en el movimiento del péndulo son la aceleración de la gravedad, la longitud del cordel y la masa. Pero, ¡alto ahí!. La masa no puede influir, porque hemos ya señalado que la caída de un cuerpo no depende de su masa. Nos quedan por tanto sólo la aceleración de la gravedad y la longitud del cordel. La cuestión básica del análisis dimensional es: ¿Cómo combinamos estas dos cantidades para obtener un número con unidades de tiempo?. Recuerde el lector que la aceleración tiene unidades de m/s2. Si dividimos la longitud del cordel entre la aceleración obtenemos un tiempo al cuadrado. Por tanto, si hallamos su raíz cuadrada ya tenemos el tiempo buscado como:
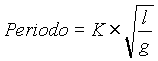
donde K es un número adimensional (es decir, que no tiene unidades). En las fórmulas físicas habitualmente aparecen factores sencillos del tipo:
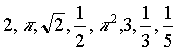
Si medimos el periodo de un péndulo y lo comparamos con la raíz cuadrada de la longitud dividida por la aceleración de la gravedad, vemos que falta un factor de aproximadamente 6. Ese factor tiene muchas posibilidades de ser el doble de pi, 6.28. Otra pista es que interviene un ángulo en el movimiento del péndulo, y el factor 2·p es usual en estos casos.
|
anterior: Ley de gravitación universal y leyes del movimiento |
siguiente: El movimiento de la Tierra |
Copyright 1996-2004 Pedro J. Hernández