La aceleración centrípeta

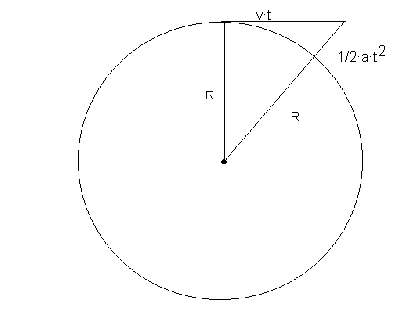
Vamos a demostrar a continuación que la objeción de "la rueda que gira" no es tan insalvable como podría parecer. Vamos a ver qué aceleración sería necesaria para mantener a un cuerpo girando alrededor de la Tierra sin que tienda a ser expelido por la rotación de ésta. En la figura 15 hacemos la misma representación generalizada que hacíamos en el caso de la figura 10 para un caso particular.

Figura 15

Y del triángulo de la figura obtenemos de nuevo:

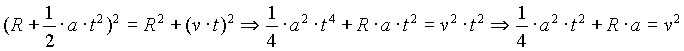
Puesto que esta aproximación es válida sólo para tiempos muy pequeños, podemos despreciar el término que contiene a t² y obtener finalmente que:

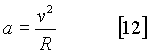
La expresión [12] es la aceleración necesaria para mantener un objeto describiendo una circunferencia de radio R con una velocidad v, y más conocida como aceleración centrípeta, o a veces llamada incorrectamente centrífuga. Aplicado a un objeto de la superficie terrestre

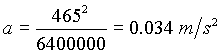
donde 465 m/s es la velocidad de rotación terrestre y calculada como:

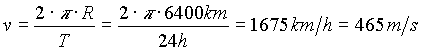
Por tanto, la tendencia del cuerpo a ser expelido por la Tierra es del orden de un 3.5 por mil de la aceleración de la gravedad que tiende a retener al cuerpo pegado a la superficie. Así, las razones que eran argumentadas antes del Renacimiento para la imposibilidad de la rotación terrestre pierden su peso con estos cálculos.

Para una deducción más complicada pero de interés histórico ver http://www.sc.ehu.es/sbweb/fisica/cinematica/circular2/circular2.htm#Deducción de la formula de la aceleración normal por Newton

otra deducción muy general en http://www.sc.ehu.es/sbweb/fisica/cinematica/circular3/circular3.htm#Movimiento circular uniforme

Copyright 1996-2004 Pedro J. Hernández