El Sistema Solar.

La objeción principal al modelo copernicano del sistema planetario era el movimiento de la Tierra. Hemos visto en las secciones anteriores cómo este movimiento es perfectamente posible sin que se produzcan los efectos temidos por los sabios anteriores a Galileo. El astrónomo y sacerdote Johannes Kepler (1571-1630) intentaba descubrir el secreto del movimiento de los planetas cuando se encontró que le era difícil encajar los datos de la órbita de Marte que había obtenido de las observaciones de Tycho Brahe (1546-1601). Las medidas astrométicas de Brahe eran las más precisas de historia anterior a la invención del telescopio, alcanzando precisiones de fracción de minutos de arco. Kepler no podía encajar los datos de Marte en una órbita circular. Después de probar algunas posibilidades formuló tres hermosas y simples leyes para el movimiento de los planetas alrededor del Sol:

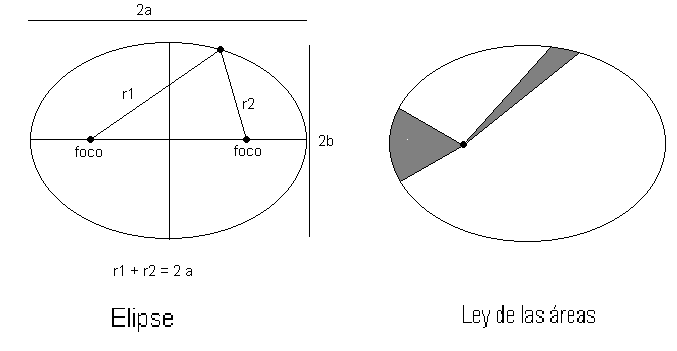
1. Los planetas giran en órbitas elípticas con el Sol situado en uno de los focos de la elipse

2. La línea recta trazada que une al planeta con el Sol barre áreas iguales en tiempos iguales

3. La razón entre el cuadrado de los periodos de rotación de dos planetas cualesquiera es la misma que la razón entre el cubo de sus distancias medias al Sol.

Figura 16. Propiedades de la elipse (izquierda) y representación gráfica de la ley de las áreas (derecha)

De las dos primeras leyes, Isaac Newton dedujo que la fuerza implicada en el movimiento planetario tenía que estar dirigida hacia el Sol, y de la tercera que esta tenía que variar con el inverso del cuadrado de la distancia. La demostración de lo primero requiere de un poco de matemáticas que van más allá de lo que pretendemos aquí. Lo segundo es más sencillo de demostrar, pero lo vamos a dejar para el lector más interesado. Las leyes de Kepler constituyen un paso definitivo para la comprensión del movimiento del sistema planetario

Tabla 3. La siguiente tabla lista información estadística del Sol y los planetas:

Más datos del Sistema Solar y de los satélites en http://www.sc.ehu.es/sbweb/fisica/celeste/solar/sistema_solar.htm

La cuestión que surge inmediatamente es, ¿cómo se han obtenido todos esos datos?. Bien, la respuesta es una larga y meticulosa observación a lo largo de la historia. En la época de Kepler sólo se conocían cinco planetas, aparte de la Tierra. Kepler encajó los datos de estos cinco planetas en un sistema solar donde todo estaba en razón de la distancia Tierra-Sol que se toma como la unidad astronómica (ua). Pero si queremos las dimensiones reales tendremos que determinar alguna distancia dentro del sistema solar. En 1671 un grupo de astrónomos franceses había medido la distancia hasta Marte de manera razonablemente aproximada, utilizando observaciones simultáneas de la posición del planeta visto desde Cayenne (Guayana Francesa) y París, estableciendo así una escala más precisa para el Sistema Solar. Durante mucho tiempo las dimensiones más precisas del sistema solar se basaron en la distancia medida al asteroide Eros, que se acerca cada 44 años dentro de una distancia de unos 22,5 millones de kilómetros. Sin embargo, con el desarrollo de las técnicas de radar se pudo determinar la distancia directamente hasta Venus. Por supuesto, que las medidas de radar exigen el conocimiento de otra medida, la velocidad de las ondas de radio. Pero eso es otro tema en el que entraremos más adelante.

Figura 17. Representación de dos posiciones arbitrarias de Venus y la Tierra a lo largo de sus órbitas.

Conocida la distancia Tierra-Venus en el caso particular en que Venus presenta una fase de cuarto, se pude relacionar con la ua como

de donde se ha deducido que la ua, es decir, la distancia Tierra-Sol es de unos 149.6 millones de kilómetros. Una vez medida esta distancia, podemos obtener datos tan sorprendentes como el tamaño o la masa solar. El sol presenta un diámetro aparente muy aproximadamente igual al de la Luna, unos 30' de arco, ó medio grado. Al igual que hicimos para la Luna

radio solar = 149,6 tan[0.25º] = 0.6527 millones de km = 652,700 km.

Un poco más de 100 veces el radio de nuestro planeta. Esto puede parecer poco impresionante, pero si tenemos en cuenta que el volumen va como el cubo del radio, el Sol tiene un volumen de 100³ o un millón de veces mayor que la Tierra, es decir, que necesitaríamos un millón de planetas como el nuestro para abarcar todo el volumen solar.

Igualmente podemos deducir la masa del Sol de la ley de gravitación newtoniana. La aceleración a la que está sometida la Tierra en su órbita alrededor del Sol está dada por:

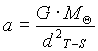
Donde la M_Q es la masa solar, y d_T-S la distancia Tierra-Sol. Pero también recordamos que la aceleración necesaria para mantener un cuerpo en una órbita circular viene dada por la expresión [12] como

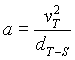
donde v_T es la velocidad de la Tierra que podemos calcular como

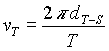
donde T es el periodo de traslación de la Tierra. Combinando las expresiones tenemos que la masa solar se pude calcular como:

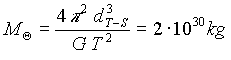
y de paso determinamos que la velocidad media de la Tierra a lo largo de la órbita es de unos 30 km/s. El lector se puede entretener en seguir deduciendo algunos datos como éste a partir de la tabla de datos del Sistema Solar.

Copyright 1996-2004 Pedro J. Hernández