Inflación caótica

    Construir un modelo de inflación es relativamente sencillo. Sólo es necesario elegir un potencial para el campo escalar que tenga un mínimo global correspondiente a un estado de vacío. Un modelo simple que puede servir como ejemplo podría ser el cam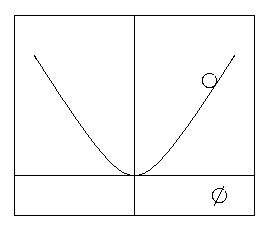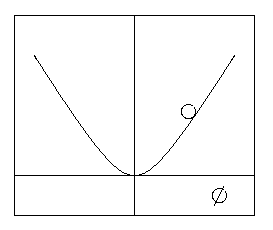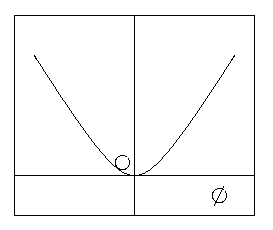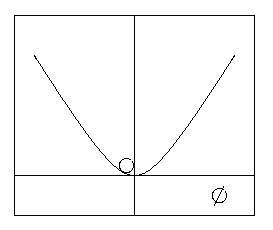po escalar de masa m (típicamente del orden de la escala de Gran Unificación ~ 10¹⁶ GeV)  , homogéneo y con mínimo de acoplamiento (es decir, sin terminos de interacción con las fuentes del tipo f ·r ) representado por la función potencial

 V(f) = 1/2 m² f²

que tiene un mínimo obvio en f = 0 (ver figura).
    El campo escalar f está sometido a la ecuación dinámica

        d²f/dt² + 3 H df/dt + dV/df = 0 [I]

    Con H la constante de Hubble. Esta ecuación puede ser generada de diversas formas*. Teniendo en cuenta que la densidad de energía del campo r_f se puede poner como

r_f  = término cinético + término potencial = 1/2 [df/dt]² + V(f)

La ecuación [I] resulta de considerar la conservación de la energía en la expansión del universo
Potencia generada por el campo escalar al aumentar el volumen del universo = Potencia consumida por el trabajo realizado en la expansión.

    dW/dt = -p dV/dt  Þ  d/dt (r_f a³) = - p_f d/dt (a³) Þ dr_f/dt = -3 H ( r_f + p_f)

siendo a el parámetro de expansión y p_f la presión efectiva del campo escalar que toma el valor

p_f = 1/2 [df/dt]² - V(f)

    La otra ecuación fundamental que debe cumplirse es la ecuación de Friedmann.

H² = [1/a da/dt]² = 8/3 p G r - K c²/a² Þ
Þ H² + K c²/a² = 8/(3 p M_p²){1/2 [df/dt]² + V(f)} [II]

Donde M_p = G^-1/2 es la masa de Planck en el sistema natural de unidades ( h = c = 1)
    Si sustituimos el valor del potencial en la ecuación [I] obtenemos

d²f/dt² + 3 H df/dt  = -m²f

Esta ecuación es análoga a la de un oscilador armónico con fricción que se escribe habitualmente de la forma (ver por ejempo Feynman Vol I. §23-2)

d²x/dt² + g dx/dt  + w₀² x = 0

    Si el campo fue en algún momento muy intenso, la ecuación de Friedman [II] implica que H tenía un elevado valor y por tanto el término de fricción sería importante y el campo se comportaría como una bola que rueda por una pendiente en el interior de un líquido viscoso (condición de rodadura lenta).
    A diferencia de la materia ordinaria, la densidad de energía del campo escalar permanecería muy aproximadamente constante, comportandose dinámicamente como una constante cosmológica que llevaría a una tremenda tasa de expansión exponencial (ver universo de de Sitter). Todo esto haría que  muy pronto se cumpliera que

r_f  ~ -p_f ~ V(f)
d²f/dt² << 3 H df/dt  ; df/dt  << m²f;  H² >> K c²/a²

ó expresado en lenguaje llano, el término de fricción es dominante (el universo se expande muy rápido), la energía cinética del campo es mucho menor que la energía potencial (rodadura lenta) y el término de curvatura es despreciable debido al gran tamaño que adquiere una pequeña región del universo después de poco tiempo (ver más abajo).
    Con estas condiciones las ecuaciones [I] y [II] se simplifican en gran medida quedando como

df/dt  = -m M_p/ 2 (3 p)^1/2
H = 1/a da/dt = (p/3)^1/2 2 (m/M_p)f

    La primera tiene la solución sencilla f  = f₀ - m M_p/ 2 (3 p)^1/2 t siendo f₀ el valor inicial del campo.
    La segunda muestra como el factor de escala del universo  a(t) crece exponencialmente como e^Ht. Esta expansión exponencial es lo que se denomina periodo inflacionario y dura hasta que el energía del campo es mucho menor que la masa de Planck (unos 10^-35 s). En dicho periodo la escala de distancia tiene que haber aumentado de tamaño en un factor e^N con al menos N ~ 60 para resolver el problema del horizonte.  El número N puede ser relacionado con el valor inicial del inflatón f₀ de la siguiente manera trivial

N = ò_f=f0 ^f=0 H dt = 2 p M_p^-2 f₀²

Y aunque el campo escalar pueda empezar con un valor mucho mayor que la masa de Planck
                         f₀   = (N/2p)^1/2 M_p > (60/2p)^1/2 M_p ~ 3 M_p

La densidad de energía puede ser bien baja comparada con la escala de Planck

r₀  ~ V(f₀) = 1/2 m² f₀² > (60/4p) m² M_p² ~ 3 10^-6 M_p⁴    para una masa m típicamente del orden de la escala de Gran Unificación ~ 10¹⁶ GeV

    Posteriormente, al final de periodo inflacionario, el campo empieza a oscilar alrededor del mínimo de energía potencial y pierde energía creando pares de partículas elementales, que interaccionan entre sí hasta crear un estado de equilibrio térmico que corresponde al punto de comienzo del Big Bang estándar.
    El escenario de inflación caótica tiene el atractivo de eliminar la dependencia de las condiciones iniciales. Así, las características principales de modelo son practicamente independientes del potencial que uno ponga para el campo escalar. Así uno puede imaginar diferentes regiones de universo del orden de la longitud de Planck con campos escalares con energía muy baja que apenas se inflan y otras con densidades de energía elevadas que llevan a crear burbujas en expansión homogéneas de hasta (en algunos modelos) ¡10^{1000000000000} cm! (Linde 2001). La forma de la energía potencial del campo puede ser cualquiera, diferente en diferentes regiones separadas por una distancia mayor que c/H (el radio de Hubble), por lo que estas regiones evolucionan independientemente unas de otras y pueden ser consideradas como mini-universos.
 

    Pero la situación es incluso más flexible que todo eso. Se puede demostrar** que fácilmente es posible que cada región se divida en varias (~20) después de un tiempo de Hubble 1/H con una densidad de energía del campo escalar mayor que la de la región incial en unas pocas (~3), repitiéndose el proceso indefinidamente, dando lugar a un escenario conocio como inflación eterna donde se crean una cantidad inmensa de regiones o universos bebé en expansión (Linde 1994, Linde 2001, Guth 2000). En cada uno de estos universos bebés, el campo escalar podría tener diferentes mínimos que implican diferentes estados de vacío que podrían dar lugar a leyes físicas diferentes a baja energía. Si este escenario correspondiera con la realidad, constituiría una base física sencilla de la aparente efectividad  del principio antrópico (Pedro J. Hernández 2000).

(*) Por supuesto esta es una manera algo artificial de derivar la ecuación [1] para mantenernos en física elemental. Definiendo la densidad de Lagrangiano del campo
L = 1/2 [df/dt]² - V(f) la ecuación [1] surge directamente de las ecuaciones de Lagrange
dL/df - d/dt dL/(df/dt) aplicadas al Langragiano total  L = L a³. (Ver por ejemplo Gordon Kane 1987 Modern Elementary Particle Physics. Addison-Wesley §2-4)

(**) El inflatón es tratado como un campo clásico. Pero por supuesto a las escalas consideradas tienen que existir efectos cuánticos, por lo que en un tratamiento semi-clásico podemos considerar fluctuaciones cuánticas dadas por el principio de incertidumbre de tal forma que

Dt DE ~ H^-1 Df_cuant  ~ 1/2p    (con h = 1 en unidades naturales)

puesto que el tiempo característico de cambio del campo escalar es el tiempo de Hubble.
Los efectos cuánticos serán apreciables en la dinámica del campo escalar cuando la variación clásica del campo sea del mismo orden de magnitud que la fluctuaciones cuánticas. Es decir, cuando

Df_clas  ~ m M_p/ 2 (3 p)^1/2 H^-1  ~  M_p²/(4 pf) ~  Df_cuant  ~  H/2p

de donde obtenemos que la condición se cumple para un valor del campo f ~ M_p^3/2/ m^1/2
    Es interesante notar que aunque el valor del campo sea mucho mayor que la masa de Planck, la densidad de energía correspondiente es considerablemente menor que ésta

r  ~ V(f) = 1/2 m² f² ~ 1/2 (m/M_p) M_p⁴ ~ 10^-4 M_p⁴

para una masa m típicamente del orden de la escala de Gran Unificación ~ 10¹⁶ GeV

    Considérese ahora lo que ocurre dentro de una región del universo con un valor incial del campo (f_i) de este orden. En un tiempo de hubble el volumen de la región se incrementará en un factor a³~ e³ ~ 20. Dicha región por tanto puede dividirse en unas 20 del mismo volumen que la región original, y en cada una de ellas el valor medio del campo será

f = f_i + Df_clas+ df

donde  df representa un salto cuántico aleatorio correspondiente a una distribución de probabilidad gaussiana con una desviación estándar Df_clas ~  Df_cuant
La estadística gaussiana implica que existe un 15.9% de probabilidad que una variable gaussiana aleatoria exceda su valor medio en más de una desviación estándar y por tanto esta es la probabilidad de que el cambio neto en el campo escalar sea postitivo, lo que implica que de las 20 regiones, hay unas 3 regiones (~ 0.159 · 20) que excederán el valor original del campo escalar. Puesto que el argumento puede ser repetido para cada una de estas regiones, uno espera que el volumen donde f > f_i aumente exponencialmente con el tiempo. Una vez se pruduzca una región con un elevado valor del campo escalar (tipicamente algo menor de 3 Mp) la reproducción de nuevos universos se empieza a producir de forma exponencial y sin límites.(Linde 2001, Guth 2000)

índice principal de Cosmología

Copyright 1996-2004 Pedro J. Hernández