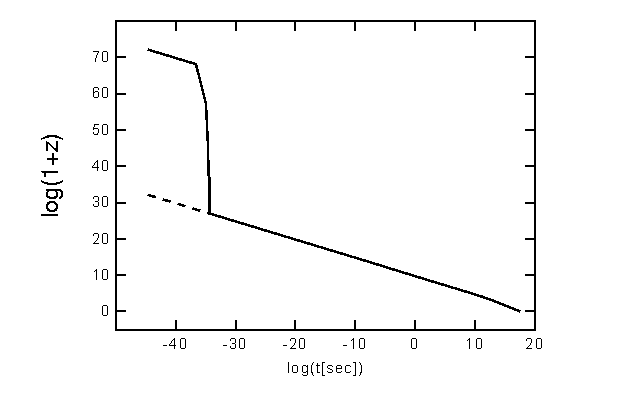
Variación del logaritmo de (1+z) frente al tiempo para un universo que pasó por una época inflacionaria. La línea discontinua representa la predicción del Big Bang estándar (figura obtenida de las notas del año 97 de Ned Wright)
En cada instante de la
historia del universo existe un distancia que determina un límite
u horizonte para el universo observable en esa época, el cual
está fijado por la distancia que ha viajado la luz desde la
singularidad inicial del Big Bang (ver horizontes
en cosmología). Este horizonte tiene el efecto de ser el
límite de distancia para la cual dos regiones del Universo
pueden estar causalmente conectadas, es decir, que una señal
luminosa haya podido llegar desde una de las regiones hasta la otra.
Cuando miramos en direcciones diferentes del cielo observamos que la
isotropía
del fondo cósmico de microondas es tan
buena como algunas partes en 100,000. El fondo
cósmico de microondas ha viajado libremente por el
universo desde la época
de la recombinación (T = 3000K), donde los electrones y
los núcleos existentes (esencialmente hidrógeno y
helio) se combinaron para formar átomos neutros (ver universo
primigenio). Desde ese instante, los fotones no encontraron la
interacción con partículas cargadas como los electrones
y pudieron moverse afectados sólo por la expansión del
universo. Por tanto, esa es una época interesante del universo
para calcular la distancia al horizonte.
El radio del horizonte de partículas para un observador situado en un desplazamiento al rojo z viene dado por:
RH =ò (1+z) c dt = òz¥ (1+z) c dt/dz dz
En un universo crítico dominado por materia tenemos que
H0 dt = (1+ z)-5/2 dz
Y por tanto
RH = 2 c H0-1 (1+ z)-1/2
La época de la recombinación se produce para z ~ 1100.
El diámetro angular de regiones de tamaño del orden del horizonte en la época de la recombinación es
dq = DH / r (ver métricas de FRW)
donde r es la coordenada comovil radial hasta la época de la recombinación. En un universo de Einstein-de Sitter esto es
r = ò 0z (1+z) c dt/dz dz = 2 c/H0 [1- (1+z)-1/2]
y por tanto
dq = 2 [(1+z)1/2-1]-1 ~ 3.6º
Esto significa que regiones del cielo separadas por más de 3.6º estaban causalmente desconectadas en la época en que la radiación dejó de interaccionar con la materia. La pregunta es por qué entonces la isotropía de la radiación es tan buena como algunas partes en 100,000 en cualquier dirección del cielo que miremos (ver fondo cósmico de microondas).
Una posible solución
a este problema de la desconexión causal lo ofrece el
escernario inflacionario. De acuerdo con
los escenarios inflacionarios, una
expansión exponencial ocurrió en el universo muy
temprano cuando habían transcurrido unos 10-35
segundos desde el Big Bang y la energía
característca rondaba los 1016 GeV
(equivalente a un tempertura de unos 1028 K)
Dicha expansión
exponencial duró una cantidad finita (y muy pequeña) de
tiempo de tal forma que las escalas de distancia crecieron en un
factor enorme que podemos poner como
a(tf)/a(ti) = eN
siendo a(tf)
el parámetro de expansión
en el momento de finalizar el periodo inflacionario, a(ti)
el parámetro de expansión en el momento inicial de
inflación y N una medida apropiada del incremento de la
escala de distancias.
En
una expansión exponencial el parámetro de expansión
evoluciona como
a(t) = a(ti) exp [Hinf (t-ti)]
Un observador después de que haya ocurrido la transición inflacionaria verá el horizonte de partículas a una distancia
rP = c ò0tf a(tf) dt/a(t) =c ò0ti a(tf) dt/a(t) + còtitf a(tf) dt/a(t)
Despreciando la contribución del universo preinflacionario y teniendo en cuenta que da(t) = H a(t) dt tenemos que la distancia al horizonte de partículas es
rP = c/H a(tf) òa(ti)a(tf)da/a2(t) = c/H {a(tf)/a(ti) - 1}
Luego rP
= c/H {eN-1}
y
el horizonte se aleja del observador durante inflación a una
velocidad superlumínica igual a
drP/dt = c/H eN dN/dt = c eN
mientras que una partícula situada en el horizonte del observador se aleja a una velocidad
v = H rP = c {eN-1}
donde se ve fácilmente que el horizonte
traspasa a las partículas que se hallan en él a
velocidad c, como debe ser siempre el caso.
Puesto que el radio de Hubble
permanece constante a una distancia c/H, todas las partículas
son barridas mucho más allá del radio de Hubble durante
el periodo inflacionario. Sin embargo, cualquier partícula que
se encontrar dentro del universo observable antes de inflación
permanecerá dentro del universo
observable después de inflación.
Veamos cuál es la tasa mínima de expansión
exponencial durante inflación para resolver el problema del
horizonte.
Si rv
es el radio del universo visible actualmente , tenemos que,
para que todo el universo visible esté causalmente conectado,
se tiene que cumplir que
rv
< rp (N) / 3 (ver horizontes
en cosmología)
donde rp
(N) es el horizonte de partículas en la actualidad cuando
ha sucedido un periodo inflacionario. Como por supuesto rv
< rp (0), donde rp (0) es el
radio del horizonte de partículas en ausencia de inflación,
se tiene entonces que una condición suficiente para librarnos
del problema del horizonte es
rp (N) > 3 rp (0)
En un universo de expansión desacelerada
tenemos rp (0) ~ c/H0
y
con inflación tendremos que rp (N) ~ a(t0)/a(tf)
c/Hinf {eN-1}
y por tanto rp (N)/rp (0) ~
[a(t0) H0]/[a(tf)
Hinf ] {eN-1}
de donde si N es grande se tiene que cumplir que N
~ log [a(tf) Hinf
/a(t0) H0]
Debemos distinguir aquí
dos épocas diferentes en la evolución del universo: una
dominada por radiación hasta una
época donde la temperatura cayó hasta ~ 104K
y otra dominada por materia hasta nuestro días. En el primer
caso el parámetro de expansión evoluciona como a(t)
~ t1/2 y en el segundo caso
lo hace como a(t) ~ tn con
2/3 £ n £
1
Para a(t) ~ tn
tenemos que la constante de Hubble evoluciona
como como
H(t)= 1/a da/dt ~ t-1
~ [a(t)]-1/n
y como a(t0)/a(t) = 1+z = T/T0
siendo T la temperatura equivalente a la distribución energética de la radiación (distribución de cuerpo negro), podemos poner entonces
N ~ log [a(tf) Hinf
/a(t0) H0]
= log [{a(tf)/a(t0)}
{Hinf /Hr} {Hr/H0}]
~
~ log [{a(tf)/a(t0)}
{a(tr)/a(tf)}2
{a(t0)/a(tr)}1/n]
donde Hr y tr
son respectivamente la constante de Hubble y la edad del
universo en la época donde la contribución de energía
de radiación empieza a dominar la dinámica del
universo.
Obtenemos un N
mínimo para n = 1 (universo vacío de materia por
ejemplo) y tenemos que
Nmin ~ log [Tf/Tr] ~ log [1028K/104K] ~ 55
siendo Tf y Tr respectivamente las temperaturas al final del periodo inflacionario y en la época donde el universo empieza a ser dominado por la radiación.
Para un universo crítico dominado por materia (n = 2/3)
N ~ log [Tf/(Tr T0)1/2] ~ log [1028K/ (3K 104K)1/2] ~ 60
es la tasa mínima de expansión exponencial durante el periodo inflacionario. El universo dobla su tamaño un mínimo de unas ¡80 veces! durante inflación.

Variación del
logaritmo de (1+z) frente al tiempo para un universo que pasó
por una época inflacionaria. La línea discontinua
representa la predicción del Big Bang estándar (figura
obtenida de las notas
del año 97 de Ned Wright)
![]() índice
principal de Cosmología
índice
principal de Cosmología
Copyright 1996-2004 Pedro J. Hernández