
El principio cosmológico (principio de homogeneidad e isotropía del universo a gran escala) restringe los posibles elementos de línea del Universo a gran escala a tres posilidades que podemos escribir por ejemplo usando ascensión recta a y declinación d como coordenadas esféricas y la distancia comóvil r y el tiempo comóvil t como coordenadas comóviles). Las coordenadas comóviles son etiquetas que ponemos a cada galaxia que pueden ser entendidas de tal manera que cada r es asignada a una galaxia que se mueve solidariamente a la expansión del universo y t sería el tiempo transcurrido desde el big bang para dicha galaxia. De forma general, el elemento de línea puede entonces ser escrito:
ds2 = c2 dt2 - a2(t) R02{ (1- k r2)-1 dr2- r2 [dd 2 + cos2d da 2]}
Donde el parámetro k, como se vió anteriormente para espacios bidimensionales "sencillos" puede tomar los valores k = 0 (espacio plano o de curvatura nula), k = +1 tenemos un espacio de tipo esférico cerrado y para k = -1 un espacio abierto de curvatura negativa. R0 es el radio de curvatura que tiene que ser el mismo en cualquier lugar del espacio por la condición de homogeneidad. El radio de curvatura está relacionado con la constante de Hubble H0 y la densidad del universo en función de la densidad crítica W (que incluye las contribuciones de materia, radiación, y densidad de energía de vacío):
R0= c H0-1 (½W - 1½ )-1/2
a(t) es el parámetro de expansión.
En el caso de un universo de densidad crítica W =1, el radio de curvatura es infinito y el elemento de línea toma la forma
ds2 = c2 dt2 - a2(t) { dr2- r2 [dd 2 + cos2d da 2]}
La distancia radial a lo
largo de una línea de tiempo comóvil constante (dt = 0)
denominada distancia física o distancia propia está
dada por D = a(t) r y es la que que aparece en la ley de
Hubble.
Un diagrama espacio-tiempo para el
caso de Universo de densidad
crítica W =1 tomando la
distancia D (eje horizontal) frente al tiempo comóvil t (eje
vertical) tiene la siguiente pinta

Donde podemos observar las líneas de mundo de los observadores comóviles situados en galaxias típicas que parten de un punto común (el Big Bang o singularidad inicial), y que son curvas debido a la desaceleración del universo
D ~ a(t) ~ t2/3 (ver universo de Einstein-de Sitter)
Las líneas grises son
líneas de tiempo cósmico (t) constante, o dicho de otro
modo, líneas que unos eventos para los cuales los observadores
que se encuentren en las proximidades de dichos eventos mediran la
misma edad para el universo.
La
línea roja representa el cono de luz pasado del observador que
se toma como en reposo en este sistema, y es en todo momento tangente
a los conos de luz. La distorsión
en la forma de los conos de luz de los observadores comóviles
se debe al efecto de la expansión. La forma del cono de luz
pasado del observador tiene la forma característica de lágrima
típica de los modelos del big bang. Ésta se debe a que
las galaxias que se encuentra más allá del radio de
Hubble en un tiempo comóvil t determinado DH (t)
= c/H(t) se mueven a la velocidad de la luz con respecto
al observador. Como H(t) aumenta a medida que nos vamos al
pasado del universo (debido a la desaceleración progresiva),
ésto significa que el radio de Hubble se hace cada vez más
pequeño a medida que nos vamos hacia atrás en el
tiempo, tendiendo a cero, con lo que la luz de una galaxia tiende la
principio a alajarse del observador. A medida que transcurre el
tiempo expansión frena y el radio de Hubble se vuelve mayor
con lo que las galaxias van entrando paulatinamente dentro del radio
de Hubble y la luz que emiten empieza a acercarce al observador.
Podemos decir que la luz se mueve con respecto a una galaxia comóvil
con una velocidad peculiar cg(t)
= drg/dt = c/a(t), lo que
podría resultar chocante a aquellos que conocen bien la
relatividad especial pero no tan bien la relatividad general.
La forma matemática exacta
del cono de luz pasado del observador puede entenderse si pensamos
que a medida que nos vamos al pasado dominará el efecto de la
expansión en el movimiento de la luz y D(t) ~ a(t) ~ ±
t2/3 mientras que la luz
que está llegando ahora al observador no estará
básicamente afectada por la expansión del universo
comportándose como en relatividad especial, de tal forma que
D(t) ~ ± t. En cualquier otro instante
podemos combinar ambos efectos teniendo en cuenta que en en el
momento actual (t=1) la distancia es cero y por tanto com D(t) ~
(±t2/3 - ±
t)
Diagramas espacio-tiempo para un universo estándar de densidad crítica con costante cosmológica. En el primer diagrama observamos cómo las galaxias comóviles "frenan" de forma similar a como sucedería en el modelo de Einstein-deSitter para empezar a acelerar posteriormente. Vemos que la típica figura en forma de lágrima del cono de luz pasado se repite en este modelo. También observamos que el radio de Hubble aumenta con el tiempo de tal forma que galaxias que en algún momento se hallan alejándose a mayor velocidad que la de la luz (superluminal) pueden en algún momento entrar en zona de expansión sublumínica (subluminal). En la figura de abajo vemos una representación en función de la distancia comóvil constante en el tiempo para cada galaxia. En este tipo de representación el cono de luz presenta un típica forma de trompeta ( r(t) = D(t)/a(t) ~ (±1 - ± t1/3)), indicando todos los eventos que hemos podido observar. El horizonte de partículas limita lo que denominamos el universo observable.
Podemos hacer una transformación y situarnos en el punto de vista del observador etiquetado por A
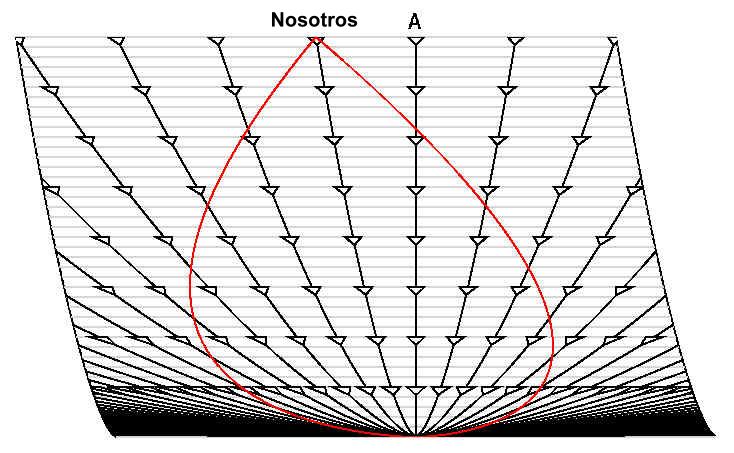
El efecto es similar al que hubieramos obtendio si las líneas grises fueran cartas de un mazo que hubiéramos desplazado lateralmente. Es importante señalar, que este tipo de transformaciones son esencialmente distintas a las transformaciones de Lorentz de la relatividad especial.
Hay que tener en cuenta que cualquier diagrama espacio-temporal que eligamos para representar un punto de vista del universo siempre estará distorsionado por el efecto inevitable de la elección de coordenadas. Pero al igual que se hacía en la proyección de Mercator, es interesante estirar o encoger el diagrama para obtener algo más intuitivo. Por ejemplo, podemos dividir la distancia física D(t) por a(t) y obtener lineas de mundo perfectamente verticales para todos los observadores comoviles (galaxias típicas), aunque con una distorsión de los conos de luz que aumenta a medidad que nos acercamos al Big Bang de tal manera que este pasa de un punto a una línea límite horizontal, tal y como ocurría con los Polos de la Tierra en la proyección plana de la superficie de la Tierra.
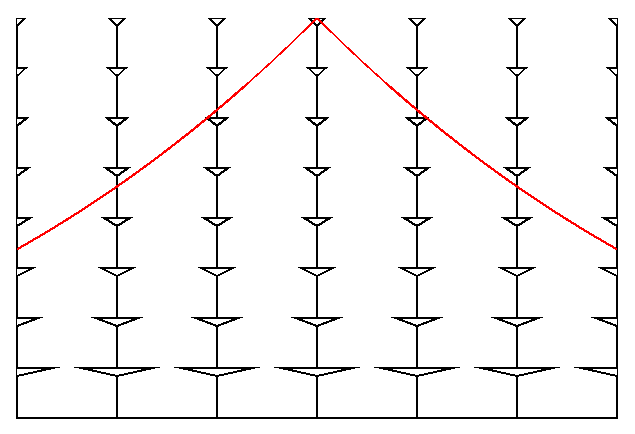
Una imagen que cubre una parte más amplia sería algo así
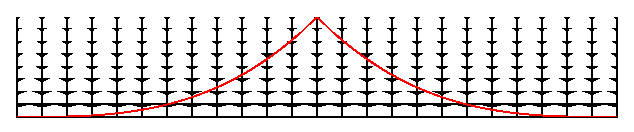
Y si por último estiramos el tiempo en el eje vertícal, de tal manera que recuperemos un cono de luz pasado formado por trayectorias luminosas rectas, obteniendo la siguiente representación
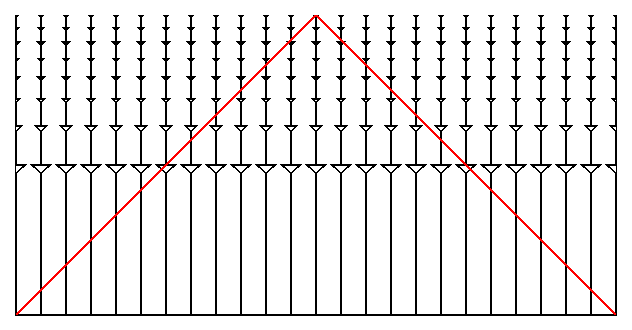
Por último deberíamos recordar que un universo de densidad crítica es espacialmente infinito y representar, para mayor claridad, una sección más amplia

Este tipo de diagramas es conocido como diagrama espacio-temporal "conforme"
Resulta entonces interesante a veces introducir la coordenada conocida como "ángulo hiperbólico" Y de tal manera que se cumpla:
dY = (1- k r2)-1/2 dr
quedando el elemento de línea como
ds2 = c2 dt2 - a2(t) R02[ dY2- f (Y ) [dd 2 + cos2d da 2]
donde
f(Y ) = sen2Y para k = 1
f(Y ) = Y 2 para k=0
f(Y ) = senh2 Y para k = -1
El elemento de línea en función de las coordenadas "conformes" (tiempo conformehy distancia comformer) del diagrama espacio-temporal "conforme" sería entonces
ds2 = a2(t) {dh 2 - R02 [ dr 2- R02 f(r R0-1 ) [dd 2 + cos2d da 2]}
con dh = a-1(t) c dt = (1+z) c dt y dr = R0 dY
En esta representación, la ecuación de los rayos luminos son las rectas
r = r0 ± (h-h0)
Un hecho fundamental a tener en cuenta es que las coordenadas comóviles r y t son esencialmente diferentes a las coordenadas habituales (x,t) que usamos en relatividad especial y que relacionamos directamente con nuestras medidad de distancia y de tiempo. Veamos cómo se comporta un diagrama espacio-temporal para un universo en expansión exponencial de de Sitter. Un modelo de de Sitter es un espacio infinito de curvatura negativa que tiene como elemento de línea en coordenadas comóviles:
ds2 = c2 dt2 - (exp [H(t0-t)] ) c H-2[ (1+r2)-1 dr2- r2 [dd 2 + cos2d da 2]
La representación espacio-temporal en función de la distancia física frente al tiempo sería
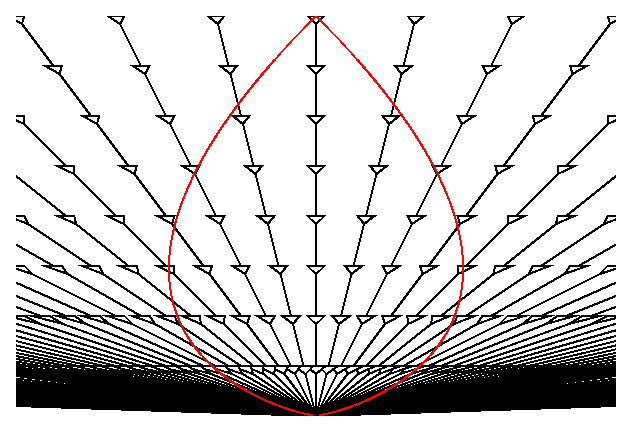
Donde podemos observar que las líneas de mundo de las galaxias van tendiendo a hacerse cada vez más horizontales a medida que nos alejamos del observador (línea vertical central). A partir de una determinada distancia, puede ocurrir que dD/dt = v = H D > c, es decir, que las velocidades aparentes de la galaxias sean mayores que la velocidad de la luz. Pero ¡cuidado con esto!. Las coordenas comóviles son un artíficio matemático que simplifican las representaciones, al igual que en un mapa geográfico producido mediante una proyección de Mercator la distancia entre dos puntos de la superficie terrestre en línea recta no se corresponde a la distancia cubierta en la superficie real de la Tierra cuando viajamos entre esos dos puntos. Hagamos una transformación de coordenas y utilicemos las coordenadas de posición y tiempo de la relatividad especial:
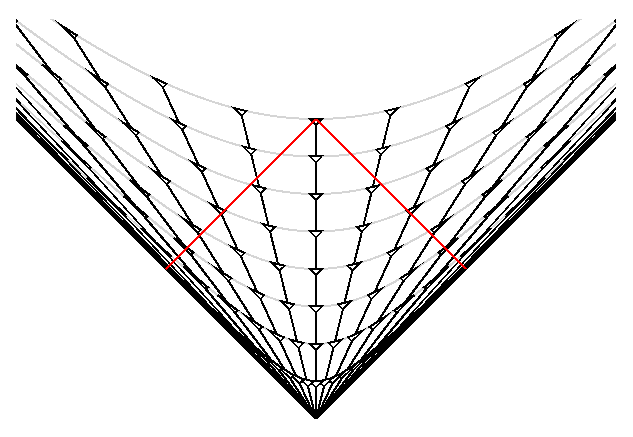
Vemos ahora que las líneas de mundo de las galaxias tienden a converger a una línea de inclinación 45º, es decir que la velocidad relativista de una galaxia nunca supera la velocidad de la luz. Las hipérbolas grises representan líneas de tiempo propio constante desde el evento del Big Bang, es decir, unen eventos donde los observadores medirían una misma edad para el universo. Además, vemo como el cono de luz pasado del observador en reposo relativo (líneas rojas) cortan las líneas de mundo de galaxias muy lejanas a una distancia relativista finita x = c t0/2. Sin embargo, la distancia D a la que se encuentran esas galaxias y que escribimos en la ley de Hubble es infinita.
Todo esto nos enseña que cuando hablamos de distancias o de tiempos en cosmología (y por extensión en relatividad general) tenemos que definir con mucha precisión lo que queremos decir y cómo lo medimos. Otra nota de precaución: la transformación de coordenadas comóviles (t,r) a coordenas relativistas de posición y tiempo (t,x) tiene sentido sólo como una aproximación cuando despreciamos la gravedad, así que no debe tomarse como significativa más que a un nivel de ejemplo ilustrativo de las dificultades intrínsecas al cambio de coordenadas en relatividad general.
![]() índice
principal de Cosmología
índice
principal de Cosmología
Copyright 1996-2004 Pedro J. Hernández