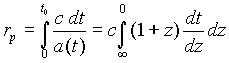
En cosmología podemos definir algunas
distancias que tienen ciertas propiedades especiales y que es
conveniente conocer.
Radio de Hubble. Distancia a la que la velocidad de recesión de una galaxia es igual a la velocidad de la luz. La velocidad de recesión de una galaxia viene dada por la relación v = dr/dt = H r. H es la constante de Hubble y r es la distancia cómovil radial.
Igualando a la velocidad de la luz tenemos que rH = c/H = 3000 h-1 Mpc, con h = H/100 .
Horizonte de partículas (radio del universo observable). Distancia a los objetos más lejanos que podemos observar en principio debido al viaje finito de la luz desde el Big Bang. Esos objetos tendrán un desplazamiento al rojo virtualmente infinito. La distancia propia puede ser definida como la distancia recorridad por la luz c dt amplificada por la expansión del universo en una cantidad directamente proporcional al cambio del factor de escala a(t0)/a(t) = 1/a(t) = (1+z). Y por tanto tendremos que
El horizonte de partículas representa el radio del universo observable.
Radio del universo visible. La radiación electromagnética más primitiva que podemos observar, el fondo cósmico de microondas, proviene de la época en la que los electrones se combinaron con protones para formar hidrógeno (a unos 3000 grados) y corresponde a un desplazamiento al rojo de unos 1100, cuando el universo tenía unos 300,000 años de edad (ver universo primigenio). Por tanto, el radio del universo visible sería
Horizonte de eventos. Corresponde a la distancia de los objetos más lejanos que podremos observar en un futuro arbitrariamente lejano. El horizonte de eventos separa aquellos objetos en su interior que podremos observar en algún momento de aquellos objetos que jamás podrán ser observados por hallarse fuera del cono de luz futuro del observador. Los modelos de universo donde la integral
converge tienen un horizonte de eventos. tmáx es el tiempo de expansión futuro que puede ser infinito o finito (por ejemplo en un universo donde empieza una fase de contracción) y t0 es la edad del universo en el momento de la observación.
Veamos las carácterísticas de estas distancias especiales en diferentes modelos de universos. Empecemos por un caso matemáticamente sencillo (veremos que conceptualmente no lo es tanto):
Expansión lineal a(t) = t/t0.
Esta
situación podría darse idealmente en un universo vacío
de materia y con una constante cosmológica
igual a cero.
La
constante de Hubble puede calcularse en este modelo como
H0
=1/a da/dt = 1/t0 y
no es más que la inversa de la edad del universo o tiempo
de Hubble. Y por tanto el radio de Hubble será
rH = c/H0
= c t0. Los objetos
que están a esta distancia se alejarán del obserador a
la velocidad de la luz. La distacia a un objeto puede calcularse
como la distancia recorridad por la luz c dt amplificada por
la expansión del universo en una cantidad directamente
proporcional al cambio del factor de escala
a(t0)/a(t) 1/a(t) =t0/t
= (1+z). Y por tanto tendremos que la
distancia a un objeto de desplazamiento al
rojo z viene dada por
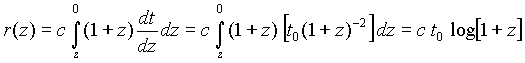
donde vemos que el
desplazamiento al rojo de los objetos en la esfera de Hubble tienen
que cumplir log (1+z) = 1 y por tanto z = e - 1 = 1.718
Observamos así algo
importante. La esfera de Hubble no es un horizonte cosmológico.
En principio podemos observar tranquilamente una galaxia situada más
allá de la esfera de Hubble, de mayor desplazamiento al rojo
que 1.718 y por tanto que se aleje a una velocidad mayor que c!!!.
Tenga el lector en cuenta que esto no contradice la
relatividad especial porque la galaxia no es capaz de viajar más
rápido que un rayo de luz que se mueva en sus proximidades.
En realidad, la velocidad de una galaxia comparada con la luz que se
mueve en sus inmediaciones es como mucho del orden de unos
centenares de km/s (su velocidad peculiar).
Vemos además que la velocidad a la que se aleja
del observador la esfera de Hubble es drH/dt
= c. Esto significa que la esfera de Hubble
se aleja del observador a la misma velocidad que las galaxia que se
encuentran sobre ella. Por tanto, la cantidad de galaxias (más
especificamente la cantidad de materia) que permanecen dentro de la
esfera de Hubble es constante con el tiempo.
Si ahora intentamos calcular la distancia al horizonte
de partículas, vemos que la integral correspondiente diverge.
Eso significa que no hay horizonte de partículas o que en
principio podemos observar todo el univero. ¿Pero cómo
puede ser esto así si el universo fuera arbitrariamente
grande?. La razón es extraña desde el punto de vista
intuitivo. Por muy alejadas que se encuentren dos galaxias en una
determinada época, siempre encontramos un tiempo finito en el
pasado donde se encontraban a una distancia lo suficiente pequeña
para que la luz pudiera viajar entre ellas en el resto de tiempo
disponible hasta dicha época. Esta es una propiedad bastante
curiosas de los modelos de expansión lineal.
La ausencia de un horizonte de eventos dependerá
de que el tiempo de expansión sea finito o infinito en el
futuro. En un universo con un parámetro de expansión
que aumenta linealmente con el tiempo, el tiempo de expansión
disponible es en principio infinito y por tanto no existe un
horizonte de eventos. En principio, si dejamos pasar el tiempo
suficiente siempre podemos recibir la luz de un objeto por muy
distante que se encuentre.
Universo
de Einstein-de Sitter. a(t) = (t/t0)2/3
El universo de tipo Einstein-de
Sitter es el caso más sencillo de universo dominado por
materia y, consecuentemente, en expansión desacelerada.
La constante de Hubble en este
caso puede ser calculada como
H0
=1/a da/dt = 2/(3 t)
Por
tanto, el radio de Hubble será rH
= c/H0 = 3/2 c t0
Los objetos que están a esta distancia
tendrán se alejarán del obserador a la velocidad de la
luz. La distancia r a un objeto puede calcularse como la distancia
recorridad por la luz c dt amplificada por la expansión
del universo en una cantidad directamente proporcional al cambio del
factor de escala a(t0)/a(t)
= 1/a(t) =(t/t0)-2/3
= (1+z). Y por tanto tendremos que la distancia
a un objeto de desplazamiento al rojo z viene dada por
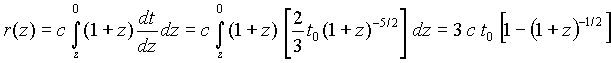
donde vemos que el desplazamiento al rojo de los objetos en la esfera de Hubble tienen que cumplir 2 [1-(1+z)-1/2] = 1 ó z = 3
La
esfera de Hubble se aleja del observador a una velocidad igual
a 3/2 c, lo que significa que las galaxias que se encontraban fuera
de esta esfera la cruzan hacia el interior a una velocidad relativa
de 1/2 c. En otras palabras, el número de galaxias dentro de
la esfera de Hubble aumenta con el tiempo.
Vemos por tanto que galaxias (superlumínicas)
que se encuentran en algún momento fuera de la esfera de
Hubble terminan por entrar y convertirse en sublumínica. La
luz emitida por esta galaxia empieza en algún momento a
acercarce al observador terminando por alcanzarlo en algún
momento.
¿Y el
horizonte de partículas?. Si calculamos la integral
rP = r (z®¥) = 3 c t0
obtenemos una respuesta
finita, lo que implica la existencia de un horizonte de partículas
y por tanto un universo observable finito.
La velocidad de recesión del horizonte de
partículas es de 3 c, mientras que la velocidad de
recesión de las galaxias es v = H0
rP = 2/3 t0 3
c t0= 2 c
lo
que implica que nuevas galaxias entran en el universo observable a
velocidad c, y a medida que transcurre el tiempo podemos ver mayor
parte del universo. A consecuencia de esto, el modelo de Einstein-de
Sitter carece de horizonte de eventos.
Universo en expansión exponencial.
Universos tipo deSitter.
a(t)
= exp [(t-t0)/t0]
Los
universos de tipo de Sitter tienen gran importancia en el escenario
conocido como inflación donde el
universo se expande exponencialmente con una tasa de expansión
tremenda (doblando su tamaño unas 80 veces en unos meros
10-33 s).
En este caso la constante de Hubble permanece realmente
constante con el tiempo pues H = 1/a da/dt = 1/t0
t0 representa
en este caso un tiempo característico de expansión que
no tiene por qué tener ninguna relación en principio
con la edad del universo. Por ello es más conveniente
escribir el parámetro de expansión como
a(t)
= exp [H (t-t0)]
Siendo
t-t0 el
intervalo de tiempo considerado.
Debido a la
constancia de la constante de Hubble, el radio de Hubble permanece
fijo. Por tanto, las galaxias saldrán del radio de Hubble a
la velocidad de la luz.
Tendremos
que la distancia a un objeto de desplazamiento al rojo z
viene dada por
r(z) = c z/H
Y los objetos que se
encuentre a desplazamiento al rojo z = 1 se alejan del
observador a la velocidad de la luz.
El horizonte de partículas se encontraría
a una distancia r (z®¥) y
por tanto arbitrariamente lejos del observador. En otras palabras,
un universo tipo de Sitter carece de horizonte de partículas
y podemos decir que todos los objetos estuvieron en algún
momento suficientemente cerca para que la luz pudiera llegar hasta
nosotros (este hecho implica que inflación resuelva el
problema del horizonte).
Sin embargo, debido a que los objetos salen de la
esfera de Hubble a la velocidad de la luz, la luz de objetos que se
encuentren más allá de la esfera de Hubble (z > 1)
empezará a alejarse del observador, y por tanto, sucesos que
ocurran ahora mismo a distancias mayor que el radio de Hubble no
serán nunca observables aún en un futuro
arbitrariamente lejano. La esfera de Hubble actúa por tanto
como un horizonte de eventos.
|
Comparación entre un modelo de expansión desacelerada (arriba) y uno en expansión acelerada (abajo). La esfera de referencia es proporcional al factor de escala. El universo observable aumenta proporcionalmente al tiempo. En un universo acelerado el universo observable aumenta más rápidamente que el factor de escala con lo que cada vez podemos ver mayor parte del universo. En cambio, en un universo en expansión acelerada (abajo), la escala aumenta de manera exponencial mientras el universo observable aumenta de la misma manera que en el caso anterior. La cantidad de objetos que podemos ver disminuye con el tiempo y el observador termina por quedar aislado del resto del universo. |
|
Una manera intuitiva de entender
la existencia de los diferentes tipos de horizontes es mediante el
uso de diagramas espacio-tiempo conformes.
En un diagrama espacio tiempo conforme se representa en el eje
horizontal la distancia comóvil r
frente al tiempo conforme t en el
eje vertical siendo
t
= ò dt/a(t)
. En esas coordenada los rayos de luz tienen
trayectorias rectas de la forma r = t0
-t siendo t0
el tiempo conforme en el momento de
observación.
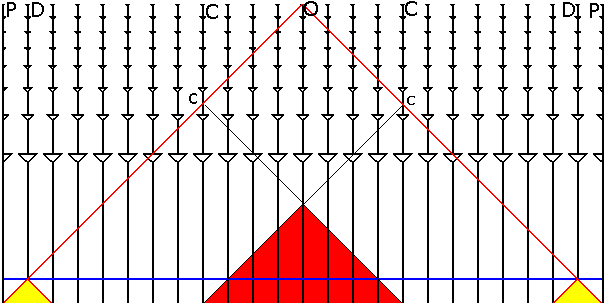
El observador se encuentra en el
punto O. El radio del universo observable es la distancia OP
formada por todos los objetos desde donde ha podido llegar la luz
(lineas rojas) hasta el observador en algún momento desde el
Big Bang (línea horizontal inferior de la figura). El momento
en que el fondo cósmico de microndas empieza a viajar
libremente sin interaccionar con la materia (indicado con la línea
horizontal azul) marca el límite del universo visible
(distancia OD).
Es
importante apreciar el hecho de que los sucesos indicados con c son
los sucesos más lejanos del observador que han podido ser
influidos por lo sucedido en su pasado mutuo. Por simple geometría
se puede ver a partir del triángulo en rojo, que esta
distancia mínima OC = OP/3. En otras palabras, objetos
que se encuentren en direcciones opuestas del cielo y situados en
menos de 1/3 del radio universo observable están causalmente
conectados.
También
se puede notar que si la integral ò
dt/a(t) diverge
cuanto t®0 estaremos en
un universo con edad conforme infinita (aunque su edad sea finita) y
por tanto sin horizonte de partículas, pues en principio los
rayos de luz pueden proceder de cualquier objeto, por muy alejado
que se encuentre. Esto se puede compreder fácilmente en el
diagrama prolongando el eje vertical infinitamente hacia el pasado.
El otro caso interesante es
cuando la integral ò
dt/a(t) converge
cuanto t®¥. En este
caso estaremos en un universo limitado en el futuro en tiempo
conforme y con un horizonte de eventos.
Modelo con constante cosmológica.
En la figura (Lineweaver
2003) se pueden
ver tres representaciones espacio-temporales
equivalente de un universo con Wm
~ 0.3 y Wl
~0.7 en el que –según
parecen indicar observaciones recientes–
nos hallamos. La línea central vertical corresponde al
observador
comóvil. Las líneas discontinuas representan las
líneas de mundo de galaxias
lejanas etiquetadas por el desplazamiento al
rojo que mide el observador hoy en día.
El primer recuadro es una representación de la
distancia propia frente al tiempo de
expansión como medido por el observador
comóvil. En el pasado inmediato del observador, el cono
de luz (light cone) es un cono (como en relatividad
especial). Pero a medida que nos vamos al pasado toma forma de
lágrima, de tal forma que la luz que nos llega hoy en día
de los objetos más lejanos estuvo alejándose de
nostros en los primeros eones de expansión, una
característica común a todos los modelos de un
universo en expansión.
En
el segundo recuadro se elimina la expansión del universo al
representar la distancia
comóvil radial (fija para cada galaxia) en lugar de la
distancia propia. En esta
representación podemos observar cómo el horizontes de
eventos se estrecha contra el observador a medida que el futuro del
universo está dominado por el efecto de la constante
cosmológica. El universo se comporta como un modelo
de deSitter, donde la esfera de Hubble actuará como
horizonte de eventos y las galaxias lejanas irán
desapareciendo paulatinamente de nuestra vista hasta que sólo
podamos contemplar las galaxias más próximas que
tienen hoy en día desplazamientos al
rojo considerablemente menores que la unidad.
El tercer cuadro es un diagrama
conforme espacio-temporal donde se puede observar cómo
las galaxias más lejanas que podemos
observar (horizonte de partículas) se hallan hoy en día
a 47 mil millones de años luz. Vemos como en sólo 13,5
mil millones de años de expansión, ha dilatado las
distancias entre las galaxia de tal forma que los fotones se mueven
por el espacio comóvil a una velocidad que en cada momento es
c/a(t) = (1+z) c.
De
acuerdo con los escenarios inflacionarios,
una expansión exponencial ocurrió en el universo muy
temprano cuando habían transcurrido unos 10-35
segundos desde el Big Bang y la energía
característca rondaba la escala de Gran
Unificación (~ 1015 GeV).
Dicha expansión
exponencial duró una cantidad finita (y muy pequeña)
de tiempo de tal forma que las escalas de distancia crecieron en un
factor enorme que podemos poner como
a(tf)/a(ti) = eN
siendo a(tf)
el parámetro de expansión en el momento de
finalizar el periodo inflacionario, a(ti) el
parámetro de expansión en el momento inicial de
inflación y N una medida apropiada del incremento de
la escala de distancias.
En
una expansión exponencial el parámetro de expansión
evoluciona como
a(t) = a(ti) exp [H (t-ti)]
Un observador después de que haya ocurrido la transición inflacionaria verá el horizonte de partículas a una distancia
rP = c ò0tfa(tf) dt/a(t) =c ò0tia(tf) dt/a(t) + c òtitfa(tf) dt/a(t)
Despreciando la contribución del universo preinflacionario y teniendo en cuenta que da(t) = H a(t) dt tenemos que
rP = c/H a(tf) òa(ti)a(tf)da/a2(t) = c/H {a(tf)/a(ti)-1}
Luego rP = c/H {eN-1}
y el horizonte se aleja del observador durante
inflación a una velocidad superlumínica
drP/dt= c/H eN
dN/dt = c eN
y
mientras que una partícula situada en el horizonte del
observador se aleja a una velocidad
v = H
rP = c {eN-1}
donde se ve fácilmente que el horizonte
traspasa a las partículas que se hallan en él a
velocidad c, como debe ser siempre el caso.
Puesto que el radio de Hubble permanece constante
a una distancia c/H, todas las partículas son barridas mucho
más allá del radio de Hubble por el periodo
inflacionario. Sin embargo, cualquier partícula que se
encontrar dentro del universo observable antes de inflación
permanecerá dentro del universo observable después de
inflación.
![]() índice
principal de Cosmología
índice
principal de Cosmología
Copyright 1996-2004 Pedro J. Hernández