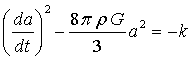
Seamos más modestos y preocupémonos por el origen de nuestro universo observable. Es decir, como hacemos siempre en ciencia, tratemos de simplificar la situación con modelos que podamos abarcar.
Primero deberíamos definir lo que entendemos por creación. En principio podríamos definir creación como la aparición de todo nuestro universo observable de "la nada". Inmediatamente nuestra intuición y prejuicios filosóficos afloran. Definamos "la nada" desde el punto de vista científico.
Escójase una región espacial y elimínese toda materia y radiación. Alguien podría decir que todavía nos queda "espacio". Pero el espacio se manifiesta observacionalmente por su curvatura. Hagamos que ésta también sea cero. Alguien todavía podría objetar que no hemos eliminado el espacio-tiempo, es decir, el marco base de nuestras medidas de posiciones y tiempos.
Para no meternos en cuestiones tan sutiles, procedamos simplemente a hacer todas las cantidades relevantes conservadas cero, es decir, carga eléctrica, número bariónico, energía, etc. Tenemos así lo que un físico de partículas denominaría un estado de vacío.
Según nuestra ecuación 1 de la dinámica de la expansión, hacer la curvatura cero implica un universo de densidad crítica o, como se ha denominado, "universo plano". Las evidencias observacionales de que vivimos en un universo de ese tipo con gran precisión son bastante convincentes.
Si observamos la deducción newtoniana de la ecuación 1, ésta implica que la energía del universo es cero. Esta observación fue utilizada por Edward Tyron en 1973 (Nature, 246, 396) para proponer que nuestro universo no es más que el resultado de una fluctuación cuántica de ese estado de vacío que Tyron identifica como espacio de un universo donde el nuestro quedaría insertado de alguna manera. Nuestro nuevo universo tendría energía cero pero repartida en iguales cantidades entre la energía positiva de la materia y radiación y la negativa correspondiente a la energía potencial gravitatoria.
Pero hay un problema grave con este razonamiento cuando lo trasladamos a su marco relativista. La energía total no es una cantidad bien definida en relatividad general: depende de lo que uno entienda por energía (Weiss & Baez 1992-98). Este punto ya fue señalado por Atkatz y Pagels (Phys. Rev. D., 25, 8) en 1982, con lo que la discusión debería mantenerse obviando este punto (el lector más exigente debería sin embargo sopesar los argumentos de Faraoni & Cooperstock 2002).
El menor intervalo de tiempo que tiene sentido medir es el tiempo de Planck. Sólo una teoría cuántica de la gravedad podrá decirnos (¡o no!) qué ocurrió o qué sentido tiene preguntarse sobre qué ocurrió con el universo antes del tiempo de Planck. Por tanto, el universo antes de ese periodo es una "caja negra" a la que deberíamos modelar de alguna forma con física bien conocida, a falta del algo mejor. Atkatz y Pagels propusieron una especie de modelo radiactivo de ese periodo del universo análogo al de la emisión de una partícula alpha por parte de un núcleo atómico. El mecanismo fundamental aquí es el efecto túnel.
El efecto túnel es un efecto puramente cuántico, por lo que necesitamos una función de onda cuántica para el universo y una especie de ecuación de Schrödinger que nos describa su evolución.
La ecuación Schrödinger aplicada al universo fue sugerida a finales de los sesenta y es conocida como ecuación de Wheeler-DeWitt. Esta ecuación describe una función de onda del universo que es en realidad un funcional (función de funciones) que especifica la geometría del universo en cada punto en el espacio tri-dimensional. La situación matemática se puede volver aquí tremendamente compleja, pero se puede uno hacer una buena idea de por dónde van los tiros elaborando un modelo sencillo de un universo descrito por la ecuación de Friedmann que representa la geometría del universo con un sólo parámetro: el parámetro de expansión o factor de escala a(t). La ecuación de Friedmann se puede escribir como
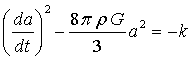
La constante k está relacionada con la curvatura desde el punto de vista de la Relatividad General y con la energía desde el punto de vista newtoniano (ver dinámica de la expansión). Atkatz y Pagels argumentan que existen sólo dos espacios con volumen finito donde tiene sentido determinar la probabilidad de atravesar una barrera de potencial por efecto túnel: un universo esférico cerrado con posible constante cosmológica (k=+1, l³0) o un universo tipo deSitter (k=0, l>0). Este último es un universo infinito, pero tiene un horizonte de eventos en su radio de Hubble rE = rH = c/H = c (3/l)1/2 , por lo que las secciones espaciales efectivas son esferas de radio igual al horizonte de eventos y por tanto un universo tipo deSitter puede ser representado como si de un espacio esférico con k=+1 se tratara. Es curioso que existan argumentos que hagan pensar que un universo tipo de-Sitter sea la condición inicial y final más natural (Carroll & Chen 2005)
Escojamos el caso k=+1 y un universo vacío con una constante cosmológica y pongamos la ecuación anterior en la forma
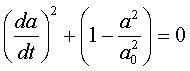
donde a02=3 (8 p r0)-1, siendo r0 la densidad de energía de vacío
Esta última ecuación puede entenderse como la energía total de una partícula de masa m=1/2 en unidades de la masa de Planck moviéndose en una dimensión con coordenada a en un potencial V(a) = [1-(a/a0)2] que se representa en la figura a continuación
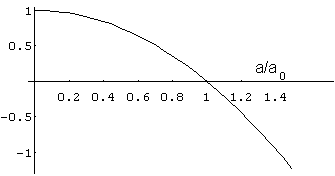
La región a<a0 es una región no-permitida o no-física. De esta forma, podemos poner el Hamiltoniano (energía total de la partícula)
H = p2 + V(a)
donde p es el momento asociado, y aplicar la regla de cuantización p = -i d/da
La ecuación de Schrödinger, en este caso un ejemplo particular de la ecuación de Wheeler-DeWitt, podrá escribirse como
H Y = [ (d/da)2+(1-a2/a02)] Y = 0
La probabilidad de una partícula que se encuentre en la región a<a0 de penetrar la barrera de potencial hasta la zona a>a0 es proporcional al factor
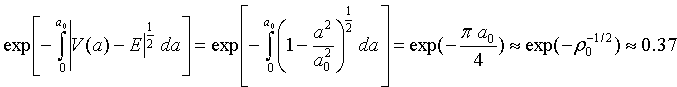
Donde podría esperarse que r0 sea del orden de la densidad de Planck que en unidades naturales es 1. El hecho de que esta probabilidad exista y sea relativamente alta (aunque en un modelo tan sencillo los números puedan no ser representativos) podría significar que nuestra "nada" modelada de esta manera (la región no-física a<a0) es inestable. Una vez el universo "se materializa" en la región a>a0 el mecanismo de inflación se encargará de aumentar su escala hasta el universo observable de hoy en día y generar la materia y la semilla de la formación galáctica. ¡Todo lo que observamos generado desde "la nada"!.
Recordemos que estamos sólo jugando con un modelo muy básico pero que nos permite hacer importantes reflexiones:
1. La pregunta que muchos consideran la pregunta filosófica por excelencia ¿por qué hay algo es vez de nada? podría tener la siguiente respuesta: la nada es una intuición de nuestro cerebro evolucionado para tener ciertos modelos de la realidad física que permitieron la propagación de nuestros genes y que en cierta manera evocan la física aristotélica y las teorías medievales del ímpetus (ver Pinker 1997, 2002 ) . Nuestra física contemporánea nos ha demostrado muchas veces que nuestros modelos matemáticos de la realidad son mucho más eficientes que nuestras intuiciones. Así, nuestra definición operacional de "nada" y un modelo cuántico sencillo nos sacan una vez más de un atolladero de nuestro sentido común. El universo puede haber surgido de nuestra "nada" operacional tal y como la hemos descrito. Uno puede encontrar la explicación satisfactoria o no, lo cual no es lo mismo que encontrarla factible o no. Por supuesto, mejorar este modelo sencillo nos puede ayudar a entender mejor el asunto o lograr una nueva perspectiva que además pudiese ser psicológicamente más satisfactoria (para modelos más elaborados ver referencias en Vinkelin 1998 y Sarangi & Tye 2005)
2. Alguien podría todavía pensar que en nuestro modelo sencillo no hemos eliminado el espacio-tiempo de la descripción. Desde luego hemos partido de hecho de un espacio-tiempo observacionalmente existente desde que hemos elegido k=+1 y no era nuestra intención eliminar todo el espacio-tiempo porque nuestro objeto era describir la creación de nuestro universo observable y no de todo el Universo. Sin embargo se han propuesto modelos posteriormente que utilizan el concepto de instantón. Digamos, hablando de manera informal, que a medida que hacemos el factor de escala a tender a cero nos aproximamos clásicamente a una singularidad (equivalente a un diagrama espacio-temporal con forma de vértice en el extremo inferior de la figura de abajo). Si sustituimos ese punto singular por una región puramente espacial se puede hacer una descripción del posterior origen por efecto túnel de un universo inflacionario (que podría modelarse para que fuese abierto o cerrado). Digamos que el instantón es "previo" al espacio-tiempo clásico (ver Vinkelin 1982, 1983, 1998) y podemos decir que hemos eliminado el espacio-tiempo clásico de la descripción del origen del universo por lo que en principio podría aplicarse al origen último del Universo. Para un modelo más sofisticado de cálculo de probabilidades de creación por efecto túnel utilizando instantones ver por ejemplo Sarangi & Tye 2005

Representación espacio-temporal de un instantón y el espacio-tiempo deSitter inflacionario creado por efecto túnel. Adaptada de Sarangi & Tye 2005
3. Otra objeción habitual es la siguiente: ¡muy bien, partimos de nada: no hay materia, radiación o incluso no hay espacio-tiempo. Pero utilizamos las leyes de la física y en concreto la teoría cuántica. Estamos poniendo algo desde el principio!. Una respuesta obvia es que ¡algo hay que poner para hacer una descripción!. Y si realmente sólo estamos poniendo las leyes cuánticas (o las leyes básicas de la física) quizás sólo estemos poniendo lo mínimo que uno puede poner en una descripción de nuestra "nada". Digamos que para hacer una descripción uno tiene que poner un espacio (aunque no necesariamente el espacio físico habitual, puede ser un espacio abstracto como el de spin) y asignar al menos un número complejo a cada punto de ese espacio. La razón de asignar un número complejo viene del hecho que tengamos que asignar una amplitud (valor de una función en ese punto) y una fase que no es más que una relación entre los valores asignados a cada punto. En el momento que decidamos que nuestra descripción no deba depender de elecciones arbitrarias y aplicando las propiedades de simetría obvias obtendremos de forma bastante directa toda la mecánica cuántica. (ver Stenger 2004).
4. ¿Y qué pasa con las causas?. La ciencia consiste precisamente en la búsqueda de causas a los fenómenos naturales. Es decir, cuál es la respuesta a la pregunta ¿qué causó que el universo atravesara la barrera de potencial o qué causó en última instancia que estuviera en el estado de "instantón" previo?. La respuesta estándar es que el proceso es incausado, ¡la creación del universo es una de esas cosas que ocurre de vez en cuando!, como la desintegración de un átomo de C-14 en nuestro cuerpo (Taner Edis 2002, Quentin Smith 1988). Digamos que es difícil quedar satisfecho con una explicación que malogra la estrategia natural de nuestro cerebro de buscar patrones y relaciones causales. Y aunque el origen incausado es una posibilidad factible, no es la única. Por ejemplo, ¿por qué no puede el universo ser causa de sí mismo por ejemplo?. (Gott & Li 1997). . También están resucitando actualmente las antiguas cosmologías eternas tipo universo cíclico (ver noticia del 26 de abril de 2002) . Para comentarios y referencias exhaustivas ver p.e. Vaas 2004.
Referencias
Pinker, S. 1997. Cómo funciona la mente. Destino. 2001.
Pinker, S. 2002. La Tabla Rasa. Capítulo 13. Paidós 2003.
Vilenkin, A. 1982, Creation of universes from nothing, Phys. Lett. B117B 25;
Vilenkin, A. 1983. The birth of inflationary universes, Phys. Rev. D27 2848.
![]() Índice
principal de Cosmología
Índice
principal de Cosmología
Copyright 1996-2006 Pedro J. Hernández