La formación de las galaxias


     El fondo cósmico de microondas es una prueba de la tremenda homogeneidad del universo (del orden de algunas partes en 100,000) en la época de la última superficie cósmica de interacción entre materia y radiación (z ~ 1100). Pero el universo actual (z <1) presenta claras irregularidades a escalas de hasta algunos centenares de Mpc –el reino de los supercúmulos de galaxias–.

    ¿Cómo inhomogeneidades tan pequeñas dieron origen a toda la estructura que observamos en la actualidad?. La respuesta a esta pregunta es lo que se denomina modelos de formación de las galaxias.

    La formación de irregularidades importantes en el gas primordial empieza con un proceso que se denomina inestabilidad gravitatoria. El mecanismo es relativamente sencillo. Las zonas del gas primordial que presentan ligeras sobredensidades tienden a acumular más materia debido a su mayor atracción gravitatoria. Las zonas de baja densidad tienden a quedarse más vacías. El fenómeno se retroalimenta hasta formar cúmulos de materia y zonas prácticamente vacías.
 
 

En la figura se puede ver una simulación en un universo con materia oscura fría de una región de unos 100 Mpc donde, partiendo de una distribución uniforme de materia (puntos rojos), se reproduce el proceso de creación de estructuras. La figura es reescalada continuamente para evitar que la expansión del universo limite la visión del fenómeno. (Fuente Martin White Homepage).

    Sin embargo, en esta imagen tan simple podrían existir mecanismos que impidieran que esto fuera así. Dos de estos mecanismos –que tienden a disgregar el material más que a acumularlo– son esenciales para mimetizar con los modelos la estructura que vemos hoy en día:

Inestabilidad gravitatoria

    Para que un cúmulo de materia forme un sistema ligado gravitatoriamente es necesario que su energía potencial gravitatoria supere a la energía térmica interna.

    La energía gravitatoria U de un agrupamiento de materia de radio característico R y masa M, es del orden de

U ~ - G M2/R

Donde G es la constante de gravitación universal.

La energía interna E de un volumen R3 es proporcional a la presión

E ~ p R3

Por tanto, para que produzca colapso debe cumplirse que

G M2/R >> p R3

Si expresamos la masa en función de la densidad r tal que M = 4/3 p r R3, la desigualdad anterior en función de la masa M se convierte en

M >> p3/2 (G-3/2r-2)

    La cantidad MJ ~ p3/2 (G-3/2r-2) –a falta de algunas constantes del orden de magnitud de la unidad– se conoce como masa de Jeans.
    Por ejemplo, en el tiempo antes de la recombinación (T~ 4000 K), podemos determinar la contribución de la densidad como

Densidad = densidad de materia bariónica + densidad de radiación

La densidad de materia disminuye como el inverso del cubo del factor de escala del universo y por tanto es del orden de

rb = 1.8791 10-29 Wb h2 (1+z)3 g/cm3 ~ 6 10-22 g/cm3

con Wb~ 0.02, h ~ 0.7 y z ~ 4000K/2.7K ~ 1500

La densidad de radiación puede determinarse como

rr = a T4 /c2= 7.56 10-22 J K-4 cm-3(4000 K)4 /(3 108 m/s)2~ 2.1 10-21 g/cm3

La presión de radiación, directamente proporcional a la densidad, puede expresarse comop = 1/3 c2rr ~ 0.6 g cm-1 s-2

Y por tanto

MJ ~ p3/2 (G-3/2 r-2) ~ 1018–1019M¤ (masas solares)

Una masa enorme comparada con la de una galaxia (~1011–1012 M¤ ). Después de la recombinación la disminución de electrones libres hace disminuir la presión de radiación, dominando la presión del gas de hidrógeno recién formado. Dicha presión viene dada por la ecuación de los gases ideales

P = n k T ~ 6 10-22 g/cm3 × 6 1023 partículas/g × 1.38 10-16 g cm3 s-2 K-1× 104 K
P ~ 5 × 10-10 g cm-1 s-2

Lo que significa que la presión ha disminuído en un factor ~ 109 y por tanto la masa de Jeans en un factor (10-9)3/2 ~ 3 10-14 lo que implica MJ ~ 105 M¤

    El hecho de que esta última masa sea del orden de la de los grandes cúmulos globulares –los sistemas autogravitantes más antiguos de nuestra galaxia– es un resultado provocativo que intrigó durante muchos años a los astrónomos.

    Calculemos ahora el tamaño característico de la región que engloba a la masa de Jeans –conocida como longitud de Jeans–, simplemente como

Antes de la recombinación l ~ { 3 (4 p)-1 Mr-1}1/3 ~ 1024 cm

Después de la recombinación l ~ 1019 cm

    El radio de Hubble por esa época estaba a una distancia del orden deDH ~ c t0 ~ 1023–1024 cm donde t0 es la edad del universo en ese momento (~ 400,000 años) y c es la velocidad de la luz.

    Se nos presenta así un problema grave. Antes de la recombinación la longitud de Jeans es del mismo orden que la escala del radio de Hubble, donde la velocidad de expansión es igual a la de la luz. Necesitamos por tanto un tratamiento enteramente relativista para entender la evolución futura de estas sobredensidades a esas escalas.

    Sin embargo, después de la recombinación, las masas que colapsan tienen longitudes características unos cinco órdenes de magnitud menor que el radio de Hubble, por lo que un tratamiento newtoniano es perfectamente adecuado en este caso.

Evolución de las fluctuaciones de densidad.

    Se define el constraste de densidad d o fluctuación de densidad r respecto a la densidad media  rm

d = (r - rm)/ rm =  dr/r

Cuando hacemos una descripción matemática de un fluido idealizado en expansión [1] obtenemos los siguientes resultados básicos:

Es habitual expresar las fluctuaciones de densidad como una suma de todas las contribuciones de todas las componentes de diferente longitud característica |x|. Uno puede enfrentarse a dicha suma como una serie de Fourier tal que

d(x) =dr/r = (2p)3/2 V-1/2S dk exp(i kx)

Que es estrictamente válida para un universo con geometría plana, lo que no será un problema puesto que a medida que nos vamos hacia atrás en el tiempo la curvatura del universo tiende a hacerse despreciable (ver el problema de la curvatura nula).
    V es aquí el volumen del cubo fundamental (V = L3) utilizado para imponer las condiciones periódicas de contorno. k es el número de onda, de tal manera que los modos de oscilación queda caracterizados por números l, m, n tal que

kx = 2 p l/L, ky = 2 p m/L y kz = 2 p n/L.

Así, cada modo de oscilación queda caracterizado por su amplitud, por su número de onda k, relacionado con la longitud de onda como l = 2 p/k

y por su fase, medida con respecto a alguna referencia

La función de correlación de dos puntos o autocorrelación x(x), definida como el exceso de probabilidad, respecto de una distribución aleatoria, de encontrar un par de galaxias separadas una distancia x. puede ponerse como

x(x) = (2p)3 V-1 S |dk|2exp(-i kx)

La cantidad importante P(k) = |dk|2 se denomina espectro de potencias. La función de correlación y el espectro de potencias están relacionados por una transformada de Fourier tal que

x(x) = ò P(k)exp(-i k x) d3k = (2p)-2 ò k2 P(k) sen (kx)/kx dk

    Uno siempre puede escoger coordenadas comóviles (que es lo más conveniente) o coordenadas físicas habituales. La relación entre ambas no es más que el parámetro de expansión, tal que dxfísica = a(t) dx y lfísica= a(t)l

    A veces es usual caracterizar una fluctuación de densidad mediante la masa situada dentro de una esfera de radio igual a una semilongitud de onda de la perturbación, es decir

M = 4/3 p rmateria (1/2 lfísica)3 ~ 2 1010 l3Mpc M¤

Donde lMpc no es más que la longitud de onda comóvil de la perturbación expresada en Megaparsecs.

Así, la masa actual de una galaxia (~ 1012 M¤) corresponde a una longitud de onda lgal~ 3.7 Mpc que es mucho mayor que el tamaño habitual de una galaxia (~ 30 kpc). Esto es debido a que estamos en el regimen lineal (|dk| <<1) donde la perturbación empieza a crecer y sigue acoplada con la expansión del universo, mientras que una galaxia actual es un sistema donde la perturbación se encuentra en régimen no-lineal ((|dk| >1). Una vez una perturbación ha entrado dentro del régimen no-lineal se desacopla de la expansión del universo, deja de expandirse y se convierte en un sistema gravitatoriamente ligado (este último proceso no del todo bien comprendido).

    Es habitual caracterizar el espectro de las fluctuaciones de densidad mediante la magnitud de cada modo de oscilación cuando alcanza el tamaño del radio de Hubble. Esto es debido a que se puede relacionar directamente la amplitud de la perturbación a partir de esta escala con la amplitud de la perturbación en el potencial gravitatorio (ver efecto Sachs & Wolfe). Más aún, esta perturbación en el potencial gravitatorio permanece invariante a partir de ese momento. Sin embargo, es importante tener en cuenta que especificar la amplitud de una perturbación de determinada longitud de onda cuando cruza el radio de Hubble implica que cada longitud de onda estará especificada en diferentes momentos.

Espectro inicial de las fluctuaciones de densidad

    Cada modo de oscilación queda caracterizado, como cualquier onda, por su amplitud, su longitud de onda y su fase. Es habitual suponer por simplicidad que las fases de cada modo son aleatorias, y por tanto no están correlacionadas unas con otras. Se suele decir que las fluctuaciones son entonces gaussianas.

   Éste puede ser relacionado con las desviaciones cuadráticas medias de la densidad ( (dr/r)2 = <d(x) d(x)> ) de tal manera que la contribución a esta desviación de un intervalo logarítmico dk/k ~ 1 está dada por

(dr/r)k2 ~ V-1/(2 p2) k3 |dk|2

que denominamos potencia de la fluctuación por intervalo logarítmico y que es idéntico a la varianza.

La pregunta ahora es cuál es el espectro inicial de las irregularidades, es decir,la contribución de las perturbaciones en diferentes escalas a su entrada en el radio de Hubble (a veces denominado simplemente horizonte). Como no tenemos idea alguna de su origen, en principio y por simplicidad debería elegirse un espectro donde cada modo de fluctuación de densidad produzca una contribución al potencial gravitatorio idéntica. A un nivel newtoniano, el potencial es proporcional a la densidad y al cuadrado de la escala de longitudes de la fluctuación de densidad, de tal modo que

(df/f)Hor~ x2(dr/r)Hor

donde el subíndice Hor indica que contamos la perturbación cuando su escala es igual a la del radio de Hubble (horizonte). Tenemos entonces que para cada escala

(dr/r)Hor ~ x-2 ~ k2

De donde concluimos que P (k) = |dk|2 ~ k

Independiente Edward Harrison (1969 Phys. Rev. 1, 2726), Y. Zel'dovich (1970 MNRAS, 160, 1p) y P.J.E. Peebles (1974 Astron.Ap., 32, 391) llegaron a esta conclusión misma.

    El razonamiento se basa en la idea de que para un espectro de potencia de forma general de ley de potencia P(k) = kn , donde a n se conoce con el nombre de índice espectral, ocurriría que para n >>1, las perturbaciones dominarían las pequeñas escalas y se formarían muchos agujeros negros que no se detectan hoy en día, mientras que si n << 1, las perturbaciones a gran escala dominarían y su contribución sería incompatible con el alto grado de homogeneidad que presenta el universo a gran escala.

    Curiosamente, el espectro de tipo Harrison-Zel'dovich es predicho de manera natural por los escenarios inflacionarios. Durante el periodo inflacionario, el universo está bien descrito por el modelo de deSitter. Este es un modelo estático del universo, en el sentido de que la constante de Hubble no varía con el tiempo. El factor de escala aumenta exponencialmente con el tiempo tal que a (t) µ exp(H t). Si hacemos una traslación temporal t ® t +T tenemos que a(t+T) µ exp (HT) exp(H t) = exp (HT) a(t). Luego reescalamos las distancias por un factor exp (HT), el universo en el instante t+T debe ser idéntico a sí mismo en el instante t. Por tanto, ninguna escala de longitud puede ser identificada por la magnitud de su perturbación de densidad en un determinado instante, y en concreto cuando ésta entra en el horizonte, y el espectro tiene que tener la misma potencia en todas las escalas.

    Inflación sin embargo tiene más problemas para predecir el valor inicial de la amplitud de la perturbación. Ésta es del orden de H2 (df/dt)-1 siendo H la constante de Hubble y f es el inflatón. La constante de Hubble depende del valor inicial del inflatón y del modelo específico de inflación. El valor inicial del inflatón se puede relacionar con el aumento del factor de escala durante el periodo inflacionario (ver inflación caótica para detalles). Este se escoge de tal manera que pueda resolverse el problema del horizonte y que sea compatible con los datos del fondo cósmico de microondas.

Tipos de perturbación

    El comportamiento termodinámico de una perturbación de densidad tiene consecuencias importantes en la evolución de dicha perturbación. Los tipos más importantes son las perturbaciones adiabáticas, isoterma y de isocurvatura.

    Una perturbación se denomina isoterma cando las irregularidades de densidad se produce en la materia pero no en la radiación. Una perturbación isoterma sobrevivirá si su tamaño característico es superior a la distancia que las ondas acústicas pueden viajar mientras el universo esté dominado por radiación.

    Una perturbación adiabática es aquella en que la perturbación se produce tanto en la materia como en la radiación de tal manera que se cumple que

(dr/r)radiación = 4/3 (dr/r)materia

Una perturbación adiabática sobrevivirá si la escala de masa es suficientemente grande para evitar la difusión por efecto de la presión de la radiación.

    Una perturbación de isocurvatura implica que la perturbación en la materia y la radiación se compensan mutuamente

drradiación + drmateria = 0

de tal manera que la perturbación no crece hasta que materia y radiación dejan de interactuar.

    El modelo estándar de formación galáctica elige las perturbaciones adiabáticas porque existe un mecanismo como inflación que genera básicamente fluctuaciones de ese tipo, básicamente debido a que el inflatón (campo escalar de que genera el periodo inflación) decae en radiación de alta energía que crea posteriormente partículas de materia, por lo que las fluctuaciones cuánticas del inflatón se transmiten a ambas componentes.

Composición del universo

    Para construir un modelo de formación galáctica es necesario especificar la composición. La opción obvia es "lo que uno ve es lo que hay", es decir, un modelo con sólo materia bariónica (protones y neutrones), fotones y neutrinos. Ningún modelo de este tipo construído hasta la fecha es capaz de reproducir las estructuras a gran escala observadas sin entrar en contradicción con otras predicciones como la densidad de bariones deducida de los cálculos de nucleosíntesis primigenia. El principal problema con un universo exclusivamente bariónico es que se necesita una amplitud inicial de las perturbaciones mayor que la permitida por las observaciones del fondo cósmico de microondas. La introducción de materia oscura que interactúa sólo a través de la fuerza débil permite que ésta se desacople de la interacción con la radiación mucho antes que los bariones, con lo que aunque el universo aparentara ser muy uniforme en el momento del desacoplamiento y compatible con lo que muestra el fondo cósmico de microondas, las perturbaciones tienen más tiempo para crecer arrastrando más tarde a los bariones para formar las estructuras. Un modelo con esta materia oscura es capaz de reproducir las principales características observadas en la distribución de galaxia.

Resulta curioso y bastante revelador que la necesidad de materia oscura aparezca en un un nuevo ámbito de las astrofísica.

Se pueden añadir dos tipos básicos de materia oscura. Materia oscura fría (CDM) y materia oscura caliente (HDM). CDM consiste en partículas relativamente masivas ( > ~1 keV) que se mueven a velocidades bajas comparadas con la velocidad de la luz. HDM consiste en partículas relativistas de baja masa.

Las fluctuaciones en la materia bariónica no tienen por qué seguir a las de la materia oscura, que puede estar distribuida de manera más uniforme. Para considerar esta posibilidad se introduce un nuevo parámetro libre b conocido como bias y definido tal que

(dM/M)galaxias = b (dM/M)total

Predicciones básicas

HDM

Si el principal componente material del universo fueran partículas relativistas de baja masa como los neutrinos, estos saldrían rápidamente de las regiones de sobredensidad, contribuyendo a suavizarlas. Así, para escalas más pequeñas que unos 13 (W h2)-1Mpc las irregularidades son completamente anuladas por el flujo saliente de neutrinos. Por lo tanto, las primeras estructuras formadas son de gran tamaño, del orden de los supercúmulos de galaxias (~ 1016 M¤) en unas estructuras aplastadas conocidas desde un estudio pionero de Zeldovich como Pancakes (crepes típicos de países anglosajones) cuyo crecimiento se vuelve no-lineal básicamente en una dimensión. Los bariones atrapados en las sobredensidades producidas pueden colisionar y disipar la energía gravitatoria, fragmentándose en objetos más pequeños de tamaño galáctico. Se dice que la formación de estructura dentro de este escenario es de tipo arriba-abajo. En las primeras simulaciones por ordenador de este tipo de escenario, se observó que para no exceder la densidad de galaxias en los cúmulos, la formación debería ser tardía (z < 1), lo que contradice las evidencias actuales de una población importante de galaxias ya formadas a desplazamientos al rojo z ~ 3-5.


 
 

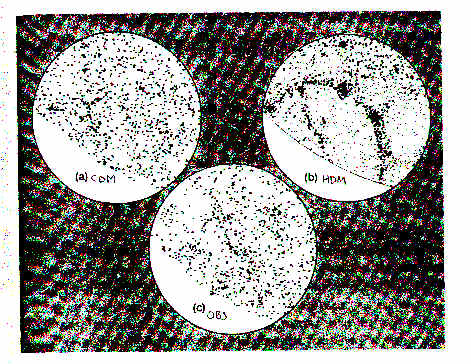
Comparación entre la distribución de galaxias observada (c), y una simulación numérica de las estructuras galácticas resultantes en un modelo de universo con neutrinos (b) y un modelo de universo con partículas más masivas y lentas (a)
 
 
 
 

CDM

    En un escenario con materia oscura fría, las partículas no abandonan tan fácilmente las sobredensidades, por lo que el proceso de homogeneización que se da en escenarios tipo HDM carece de importancia aquí, sobreviviendo incluso las fluctuaciones de densidad en pequeñas escalas. Sin embargo sí que existe un mecanismo de amortiguamiento del crecimiento de las fluctuaciones de materia inducido por las oscilaciones de la densidad de energía de la radiación que continúa hasta que el universo pasa a estar dominado por materia (z < ~ 104). Por tanto el espectro de potencias será tipo Harrison-Zeldovich con tendencia asintótica a pequeñas escala (k ॠ) a un espectro de tipo P(k) ~ k-3. En este escenario los primeros objetos en colapsar corresponden a escalas subgalácticas. Estos podrían ser halos de materia oscura que acumulan de forma gradual más materia o que crecen de forma repentina al fundirse con otros halos. Este escenario es de tipo abajo-arriba, formándose primero estructuras galácticas que posteriormente van interactuando gravitatoriamente para formar los cúmulos y supercúmulos. Este proceso podría empezar a un desplazamiento al rojo relativamente reciente pero compatible con las observaciones (z > ~ 3).

    Una amplia variedad de modelos de materia oscura comparten ciertas características comunes que explican el proceso básico de formación galáctica. El gas, bien mezclado con la materia oscura, participa del colapso de los primeros halos, calentándose hasta la temperatura de los propios halos y posteriormente enfriándose por procesos radiativos de tipo bremsstrahlung, recombinación o excitaciones por colisión y posterior emisión de luz, procesos mucho más eficientes en el pasado cuando el universo tenía mayor densidad. La nube en colapso adquiere cierto momento angular debido a la aesfericidad general de la perturbación y a los torques gravitatorios de grumos de materia próximos. Así, el colapso inicial produce una disco gaseoso, que una vez sostenida por fuerzas centrífugas empieza a fragmentarse en estrellas, un proceso no muy bien comprendido. Dos de estas galaxias primordiales pueden fundirse, en un proceso que distorsiona las órbitas de gas en el disco creando una compoente esferoidal. Esto explica de manera sencilla por qué existen dos tipos básicos de galaxias: con forma de disco y esferoidales. También explica de manera elegante por qué exite un límite superior a la luminosidad de una galaxia. Los halos de mayor tamaño se forman más tarde cuando los procesos de enfriamiento son menos eficientes. Por tanto, las fluctuaciones más masivas no han tendio tiempo de enfriarse y fragmentarse para formar galaxias.

    El escenario de materia oscura fría con energía de vacío añadida (WM ~ 0.3 y Wl ~ 0.7) parece simular bastante bien las características principales de las estructuras galácticas observadas y es compatible con una amplio rango de observaciones, como la amplitud del espectro de potencias de las fluctuaciones en el fondo cósmico de microondas, la posición de los picos Doppler, la abundancia de cúmulos clasificados por sus luminosidades en rayos X, etc. Sin embargo, los modelos de materia oscura no están libres de problemas (ver Peebles 2002)
                                z = 3                    z =1                    z = 0

Simulación de la formación de estructuras en diferentes modelos del universo. La primera fila corresponde al modelo preferido actualmente (W0 = 0.3, Wl = 0.7). La segunda y tercera fila corresponden a dos variante del modelo de Einstein-de Sitter (W0 = 1) con espectros de potencias diferentes. La cuarta fila es un modelo de universo abierto con W0 = 0.3. Las tres columnas corresponden a instantáneas en diferentes épocas del universo. Fuente Baugh & Frenk 2001. Encyclopedia of Astronomy & Astrophysics.

 


 

 

 

 

 

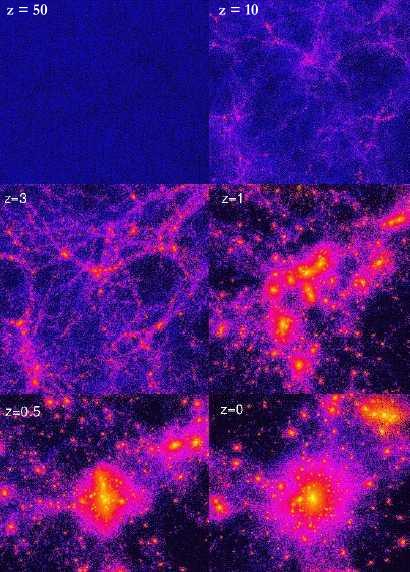
Simulación de alta resolución de la formación de un halo de materia oscura. Fuente Baugh & Frenk 2001. Encyclopedia of Astronomy & Astrophysics.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
  Evolución temprana de las fluctuaciones de densidad en un universo con materia oscura

    Vamos a fijarnos en una pequeña región de un universo básicamente homogéneo donde se produce una perturbación adiabática. Como hemos visto, en tal tipo de perturbación todos los componentes (materia y radiación) resultan afectados de manera similar (aunque la radiación es afectada en un factor 4/3 con respecto a la materia).

    Partimos de una perturbación con el siguiente perfil básico

   

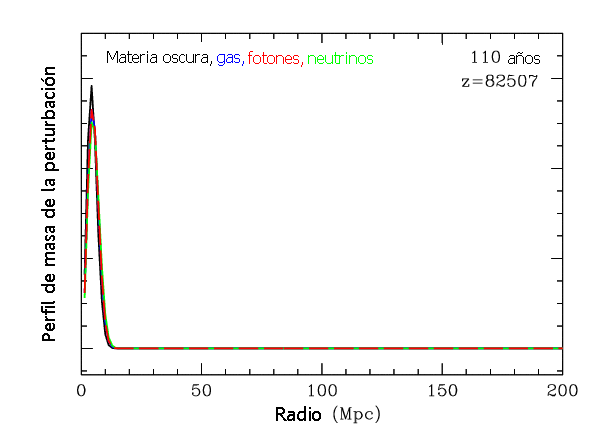
     Donde la escala de distancias en Mpc representa la separación medida en el momento actual después de producida la expansión. 

    El perfil de masa de la perturbación escala como la densidad multiplicada por el cuadro del radio. 

    Veamos lo que ocurre a continuación:

    Los neutrinos (en verde) no interaccionan con las otras componentes y son demasiado ligeros y rápidos como para quedar gravitacionalmente ligados, por lo que huyen de la zona de la perturbación disminuyendo su densidad rápidamente.

    La materia oscura fría (en negro) formadas por partículas pesadas y lentas va quedando atrapada en la perturbación y atrayendo más materia oscura de los alrededores.

    El gas (en azul) está en forma de plasma, por lo que los fotones (en rojo) interaccionan de manera significativa con éste, aumentando rápidamente la presión que supera en gran medida a la contribución de la densidad. Este aumento de presión trata de equilibrarse con el medio exterior creándose un frente esférico de ondas sonoras (ver animación) que se traslada a algo más de ¡la mitad de la velocidad de la luz!.

    Después de unos 10,000 años, las contribuciones relativas de cada componente quedan como se ve a continuación (la contribución de materia oscura es en realidad un factor 5 mayor y la de la radiación un factor 4/3 que no se han tenido en cuenta).

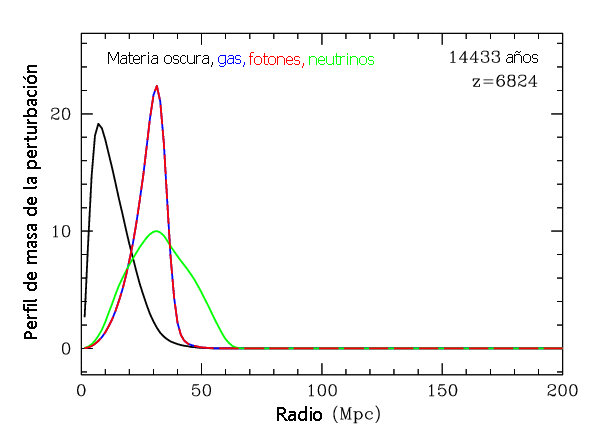
    El mismo proceso continua durante los próximos 350,000 años. Los neutrinos se dispersan y la perturbación en el plama y los fotones continua propagándose como onda sonora. La materia oscura ocupa el centro de la perturbación inicial abandonado por neutrinos y fotones. La atracción gravitatoria provocada tira de la materia oscura del entorno aumentando la longitud característica de la perturbación.

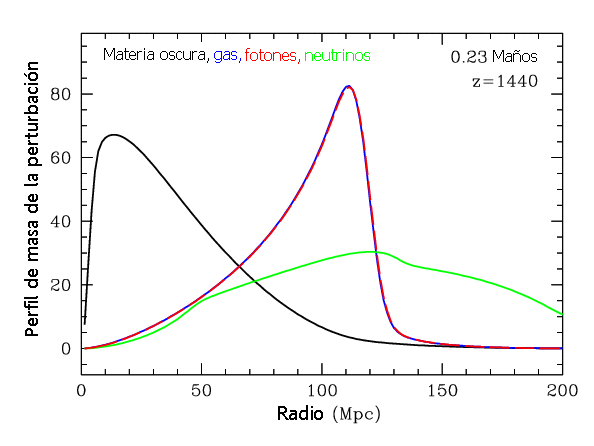
    Cuando el universo tiene unos 380,000 años, la temperatura ya no es suficientemente alta para mantener el plasma de protones y electrones y estos se recombinan en átomos de hidrógeno neutros. Los fotones dejan paulatinamente de interaccionar con la materia, la presión desciende y la onda sonora se vuelve más lenta.

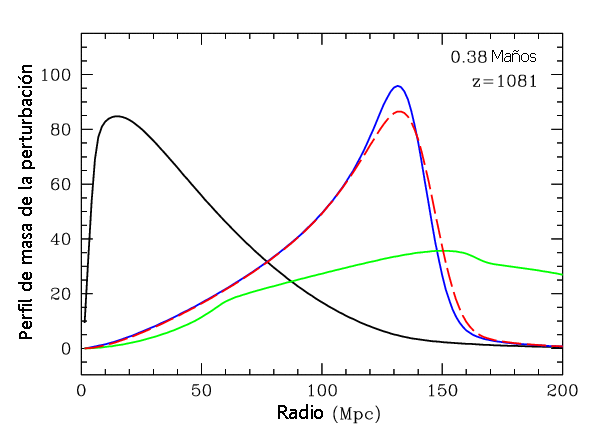
    El proceso continua y los fotones empiezan a dispersarse, suavizando la perturbación tal y como sucedió con los neutrinos anteriormente. Estos fotones viajan libremente perdiendo energía  hasta la actualidad donde los podemos detectar como el fondo cósmico de microondas.

    La onda sonora sigue perdiendo velocidad empezando a diluirse.

    Sólo la materia oscura permanece en el centro de la perturbación, extendiéndola hasta unos 150 Mpc.

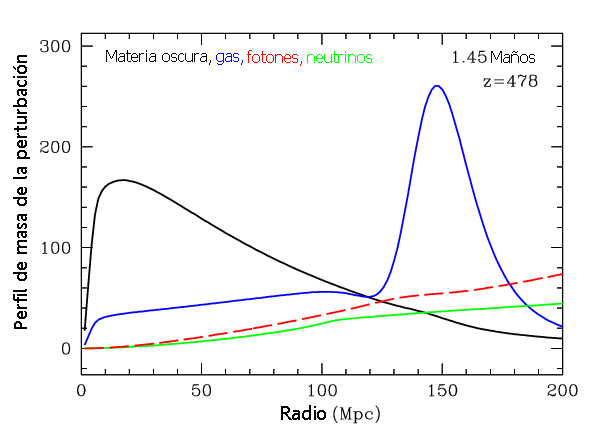
    A medida que transcurre el tiempo, el influjo gravitatorio de la materia oscura atrae al gas y ambas componentes tienden a seguir un mismo perfil (y por tanto no hay bias y la materia visible es una buena trazadora de la masa en su conjunto).

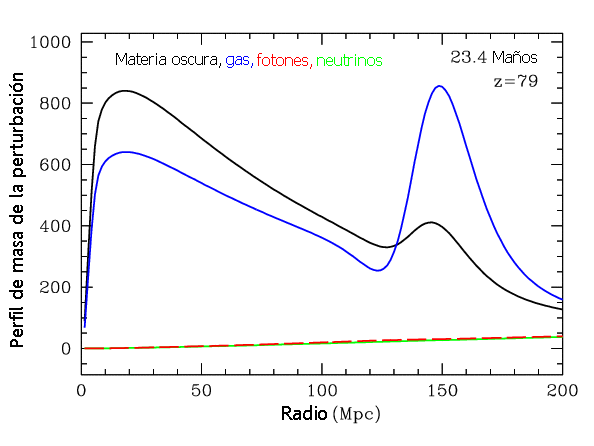
    La influencia de perturbación esférica de gas formada por la onda sonora se deja notar sobre la materia oscura  y se forma los que se denomina pico acústico, cuya magnitud resulta suavizada por la influencia gravitatoria de la materia oscura que al principio carece de ese pico (recordemos que ésta supera al gas en una relación 5 a 1).Ver animación del proceso entero.

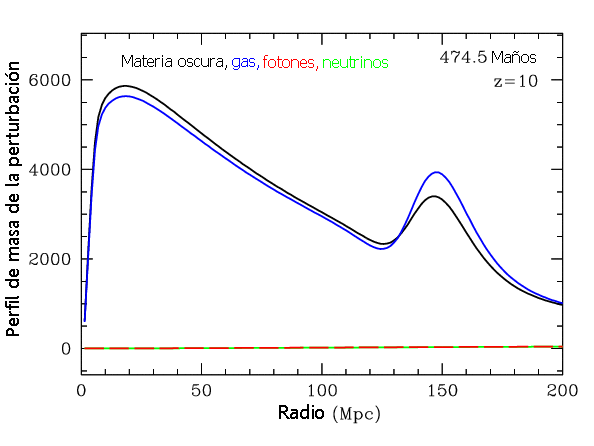
    El perfil de masa nos puede dar una idea equivocada de la importancia relativa del pico acústico de 150 Mpc. Esto puede ser mejor apreciado en una representación directa de la densidad.

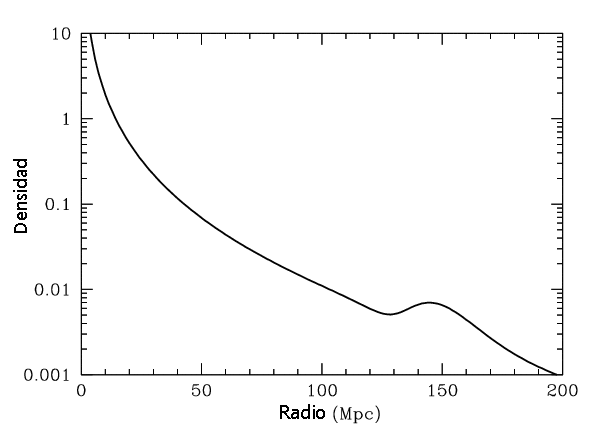
    Apreciamos que el pico acústico representa un contraste de densidad del 1% del producido en el centro de la perturbación (ver animación del proceso entero).

Las galaxias se forman en las zonas de sobredensidad de materia, con lo que en los surveys de galaxias se observa (a través de la función de correlación) un exceso de éstas en escala del orden de 150 Mpc a partir de los grandes núcleos de las estructuras situado en el centro de la perturbación original.

Alternativamente, si uno trabaja con el espectro de potencias P(k), el efecto se muestra como una serie de oscilaciones acústicas.

 

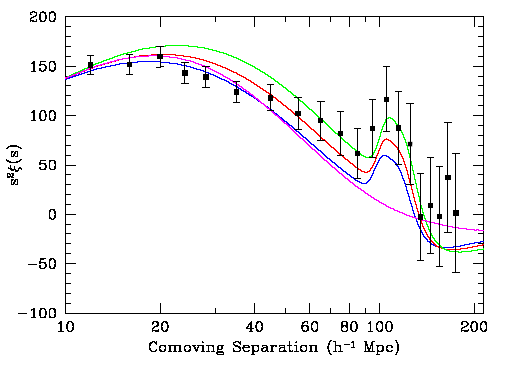    Relación con el Fondo Cósmico de Microondas

    El proceso físico explicado anteriormente es el mismo que genera las fluctuaciones detectadas en el fondo cósmico de microondas (explicadas en esta página). El fondo cósmico de microondas está formado por fotones que abandonaron el plama alrededor de z = 1000 y en los que quedaron impresas las huellas de las perturbaciones de densidad en el gas.

     El hecho de que los fotones hayan abandonado la perturbación esférica de 150 Mpc produce un máximo de variación de la temperatura del fondo cósmico entre dos regiones del cielo separadas angularmente algo menos de 1º.

    Sin embargo, conviene considerar dos diferencias básicas.

[1] Este análisis está realizado en detalle y de una manera pedagógica en excelentes referencias. Recomiendo especialmente Bowers R.L. & Deeming T. Astrophysics vol. II. Jones And Bartlett publishers. 1984. §31.1 para una somera introducción y Kolb, E.W. & Turner, M.S. The Early Universe. Addison-Wesley 1990.§9.3 para los aspectos más relevantes. Si se desea un tratamiento con gran detalle la obra maestra de este asunto es P.J.E. Peebles The Large Scale Structure of the Universe. Princeton Series in Physics. 1980. Un tratamiento bastante completo pero algo más manejable puede encontrarse en J.P. Ostriker. Development of Large Scale Structure in the Universe. Academia Nazionale del Licei. 1991.

índice principal de Cosmología

Copyright 1996-2005 Pedro J. Hernández