La dinámica de la expansión y el problema de la masa oscura

[índice de contenidos de cosmología]: [resumen][introducción][el principio cosmológico][el universo en expansión][El significado de la expansión][La dinámica de la expansión y el problema de la masa oscura] [El universo primitivo][Conclusiones][Poscriptum][Bibliografía]

     La obtención de las ecuaciones que rigen la evolución del universo puede hacerse con argumentos de la física clásica y utilizando cálculo sencillo al alcance de cualquier alumno de bachillerato. Esta posibilidad es debida al principio cosmológico: condición de homogeneidad e isotropía del universo a gran escala que nos permite utilizar la dinámica newtoniana como una excelente aproximación.
    Si elegimos una región esférica del universo, lo suficiente grande para que la condición de homogeneidad e isotropía sea una buena aproximación, pero lo suficiente pequeña para que las velocidades de alejamiento de las galaxias se mantengan muy por debajo de la velocidad de la luz, un famoso teorema nos asegura que podemos ignorar las fuerzas gravitatorias producidas por el resto de la masa del universo y aplicar la aproximación newtoniana de la relatividad general a dicha región esférica.
    Así, si imaginamos una galaxia en el mismo borde de la esfera que se mueve con velocidad v, podemos aplicar el principio de conservación de la energía en analogía al lanzamiento de un proyectil desde la superficie terrestre como:

energía cinética + energía potencial = constante

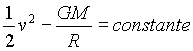
donde R es el radio de la esfera, G la constante newtoniana de gravitación y M es la masa que se encuentra en el interior de la esfera elegida. Según las observaciones disponibles hasta el momento podemos afirmar que una esfera del orden de unos pocos centenares de Mpc cumpliría esa condición de homogeneidad e isotropía con gran precisión.
    Podemos poner la masa del interior de la esfera en función de la densidad media  r como M= 4/3 p r R³, y la velocidad de expansión como v=dR/dt. Eligiendo adecuadamente el valor de la constante relacionada con la energía obtenemos la siguiente ecuación (ec.1) para la evolución del parámetro R(t):

v² = [dR/dt]² = 8/3 p G r R² - K c²             (ec. 1)

Donde c es la velocidad de la luz. Ahora la nueva constante adimensional K que aparece en la ecuación anterior está relacionada con la geometría del universo. Por supuesto, ésta no tiene más interpretación en la aproximación newtoniana que la de una mera constante de integración (asociada a la energía por unidad de masa de una partícula como una galaxia). Sin embargo, esta última ecuación diferencial es exactamente la misma que se hubiera obtenido de un tratamiento rigurosamente relativista, donde la constante K sí que tiene un significado preciso:
 

    Universos con K£0 se denomina abiertos. La constante K está íntimamente relacionada con la densidad media de materia del universo. Si hallamos el valor de la densidad para la cual K = 0 obtenemos, por sustitución en la ec.1 y simplemente despejando:

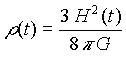
donde H(t) no es más que la constante de Hubble para cualquier instante t del universo , es decir H = v/R. Ésta es la denominada densidad crítica. En el presente del universo, la densidad crítica es

r₀ = 3H₀²/8pG = 1.8791 h² 10^-29 g/cm³

siendo h la constante de Hubble en unidades de 100 km/s/Mpc. En términos más intuitivos, esta densidadcorresponde a una densidad tan baja como la de la masa de 5-6 átomos de hidrógeno por metro cúbico.

    Se suele definir un parámetro de densidad W como la relación entre la densidad del universo en unidades de la densidad crítica (W = r/r₀) . Si la densidad de materia actual del universo es igual a la densidad crítica, en otras palabras, si W = 1, estamos en el caso de un universo de geometría espacial plana. Éste es el denominado modelo de Einstein-de Sitter y es el más sencillo de todos los posibles. Sin embargo, aunque las observaciones actuales apuntan a un universo plano con W = 1, también apuntan a que la componente principal del universo no es materia, sino algún tipo de energía oscura todavía por determinar.

    A veces nos puede confundir el término R(t), puesto que en principio su elección es arbitraria. En un universo cerrado de geometría espacial esférica se podría relacionar con el "radio del universo", pero en los otros dos casos esta noción tiene aún menos sentido si cabe. Se suele arreglar esta posible confusión haciendo

R (t) = a(t) R

Donde a(t) es un factor adimensional que se conoce como parámetro de expansión o factor de escala, y que ya no depende de los objetos concretos que se elijan.

Podemos definir  a(t₀) = 1, donde t₀  es el momento presente y fácilmente llegar a la ecuación de evolución del parámetro de expansión, siguiendo la ec.1.

(da/dt)² - 8/3 p G r a² = constante

Denominada muchas veces Ecuación de Friedmann.

y que se suele expresar como

H² = [1/a da/dt]² = 8/3 p G r - K c²/a²

    Otra ecuación fundamental en el estudio de la dinámica proviene del la primera ley de la termodinámica (principio de conservación de la energía). Para un volumen V = 4/3 p a³R³que contiene una masa M, tenemos que la energía interna viene dada por

E =M c² = r V c²

    Siendo r la densidad media en el volumen V y c la velocidad de la luz. Para una expansión adiabática (sin intercambio de calor) de dicho volumen tiene que cumplirse el primer principio de la termodinámica de tal forma que la variación de la energía interna sea igual al trabajo realizado por la expansión (*).

    dE/dt = -p dV/dt  Þ  d/dt (r c² a³) = - p d/dt (a³) Þ dr/dt = -3 H ( r + p/c²)

Que es otra ecuación importante.
    Conocidad entonces la presión en función de la densidad, lo que se denomina ecuación de estado p = p(r), podemos resolver las ecuaciones y hallar todos los parámetros relevantes en función del tiempo: a(t), H(t), r(t) y p(t)
    Las ecuaciones de estado más típicas corresponden a:

Tipo m) Polvo o materia fría.                     p/c² << r
Tipo r) Radiación o materia caliente.          p = 1/3 r
Tipo l) Constante cosmológica                  p = - r
Tipo Q) Quintaesencia                                p = wr con -1< w <0
 
 

    Si la densidad de materiamactual del universo es igual a la densidad crítica, estamos en el caso de un universo de geometría plana. Éste es el denominado modelo de Einstein-de Sitter y es el más sencillo de todos los posibles. Precisamente esta simplicidad llevó a la mayoría de cosmólogos de los últimos años a pensar que éste debe ser el caso para el universo que habitamos. Como ha señalado Richard P. Feynman: "lo más simple puede ser no tener nada, y la naturaleza es mucho más inventiva que todo eso". Existe sin embargo un argumento teórico de mayor peso. La ec.1 junto con una ecuación razonable de estado para la materia y la radiación conducen a un hecho bien curioso: cualquiera que sea el valor actual de la densidad, ésta se aproxima a la densidad crítica a medida que nos adentramos en el pasado del universo. Para que el lector se haga una idea, si extrapolamos las ecuaciones hasta que el universo tenía un solo segundo de vida, la densidad se aproxima a la crítica con una precisión de hasta la decimosexta cifra decimal. En el Modelo Clásico del Bing Bang no hay explicación para el hecho de que el universo tuviera necesariamente que "nacer" tan próximo a la geometría plana, y por eso se conoce a este hecho como "el problema de la curvatura nula", ya señalado en 1979 por Robert H. Dicke y P.J.E. Peebles de Princeton. Una posible solución a este problema nos la sugiere el escenario inflacionario comentado anteriormente. Pero, a lo que vamos: ¿qué tienen que decir las observaciones sobre la densidad actual del universo?.

    Desde los años treinta se sabe que las velocidades peculiares de las galaxias en cúmulos corresponden a una masa total del cúmulo de aproximadamente un orden de magnitud mayor que el total de toda la materia luminosa observada dentro de las propias galaxias (ver materia oscura para más detalles). También, desde los años sesenta se ha observado una situación similar en las partes exteriores de las galaxias espirales y al menos en algunas elípticas. Antes de 1980 se asumía habitualmente que esta "materia oscura" era materia ordinaria en alguna forma no detectable como gas, estrellas de baja masa y cadáveres estelares del tipo enana blanca o agujero negro. Sin embargo, los años ochenta trajeron a escena otra fascinante idea: que la materia oscura está formada por neutrinos o alguna forma más exótica de partículas aún no descubierta en los laboratorios de altas energías. La naturaleza de esta materia oscura parece uno de los grandes retos de la cosmología actual. Otra posibilidad a considerar es que la física gravitacional falle al aplicarla a escalas superiores a la de las galaxias (tal y como la dinámica alternativa MOND), aunque no hay que olvidar que la Relatividad General nos ha dado una buena descripción del fenómeno de dispersión de la luz de una galaxia lejana por la concentración de galaxias de un cúmulo interpuesto en nuestra la línea de visión, efecto conocido como lente gravitatoria, que pone en juego escalas de unos 100 Kpc, es decir, superiores en un orden de magnitud al tamaño de una galaxia típica.

    El problema de la materia oscura ofrece un ejemplo fascinante de la manera en que las ideas evolucionan en la ciencia. En los años sesenta habían pocos debates teóricos acerca del valor de la densidad de materia del universo, pues en general era considerado un problema puramente observacional. Sin embargo, a partir de los ochenta se ha instalado con fuerza entre la comunidad de cosmólogos la creencia en que la densidad del universo tiene que se igual a la densidad crítica, es decir, la idea de que nuestro universo es descrito por el modelo de Einstein-de Sitter. Esto ha sido así, en parte por la influencia de algunas coincidencias numérica ya mencionadas anteriormente, en parte por el éxito durante los ochenta de los modelos de materia oscura en las teorías de formación de las galaxias, y en mayor parte por el desarrollo del modelo inflacionario, que requiere una densidad igual a la crítica y que representa un atractivo escenario con numerosas partículas candidatas a formar parte de la materia oscura, surgidas de los modelos de gran unificación dentro de la elegante teoría cuántica de campos.

    Hasta la fecha, todo tipo de observaciones sitúa el rango de estimación de la densidad actual del universo entre una centésima y un par de décimas de la densidad crítica. Por un lado tenemos el exitoso modelo de la formación de los elementos ligeros en el universo primitivo o nucleosíntesis primigenia. Los cálculos demuestran que, para obtener las cantidades de elementos ligeros observadas actualmente, la densidad de materia ordinaria (técnicamente denominada materia bariónica) no puede ser mayor de aproximadamente una décima parte de la densidad crítica. Por otro lado, las estimaciones dinámicas del movimiento de las galaxias en grandes cúmulos, aunque muy complejas, son bastante consistentes con el hecho de que la densidad no puede ser mayor que un 1/3 de la densidad crítica. Solamente estimaciones del campo de velocidades galácticas en movimiento a gran escala parecieron en algún momento favorecer un valor próximo a la densidad crítica.

    Se alude muchas veces al problema de la masa oscura como uno de los handicaps del Modelo Estándar, pero esto sólo sería un problema serio si se demostrara que no existe manera plausible de describir las estructuras de materia que observamos en la actualidad. De momento existen modelos de la formación de estructuras galáctica con todos los rangos posibles del parámetro de densidad y con todo tipo de materia, tanto ordinaria como exótica. Si bien ninguno ha "salvado las apariencias" satisfactoriamente, el marco teórico (basado hoy en día en las simulaciones con grandes ordenadores) tiene aún un amplio margen de posibilidades, y las observaciones no son todavía todo lo numerosas y precisas que sería de desear.

    Por último me gustaría poner un ejemplo ilustrativo de la gran interacción que existe hoy entre la ciencia de lo muy grande (la Cosmología) y la ciencia de lo muy pequeño (la física de partículas). El primer candidato a materia oscura no bariónica fue una familia de neutrinos con una masa en reposo de unas decenas de electronvoltios (abreviado eV). La densidad actual de neutrinos está fijada perfectamente por la temperatura actual del fondo cósmico de radiación y es de unos 113 neutrinos por centímetro cúbico. Teniendo ahora en cuenta que las observaciones muestran que la contribución de los neutrinos a la densidad de materia no puede ser mucho mayor que la densidad crítica, nos encontramos con que la masa de un neutrino está limitada a unos 70 eV. Estamos dando un límite superior a la masa de una partícula fundamental usando observaciones puramente cosmológicas. Además, los cálculo de la nucleosíntesis primordial sólo son compatibles con las observaciones de las abundancias de elementos ligeros si y sólo si la familia de neutrinos tiene exactamente tres miembros: el neutrino electrónico, el muónico y el taúnico. Las medidas del CERN (centro europeo de investigaciones nucleares) confirman la existencia de tres tipos de neutrinos, y sitúa la masa del más pesado, el neutrino electrónico, por debajo de los 9 eV (dato de 1993). Esta última medida desplazó la atención de los cosmólogos hacia otro tipo de partículas más exóticas, puesto que con una masa tan modesta, la contribución neutrínica no sería suficiente para alcanzar una densidad igual a la crítica. Además, los modelos de formación galáctica con neutrinos masivos fracasaron completamente en la simulación de la estructura a gran escala que se observa actualmente en los mapas galácticos. Sin embargo existen algunos modelos mixtos de materia bariónica y neutrinos masivos (con masas del orden de 5-7 eV) que podrían tener algo que decir todavía.

Más información en

Materia oscura
Neutrinos en Cosmología

(*) Aunque hemos derivado la ecuación correcta de esta manera relativamente sencilla, los razonamientos que impliquen conservación de la energía en un universo en expansión no están libres de problemas conceptuales (Harrison, Edward. 1995). El lector debería recordar que toda nuestra deducción está basada en argumentos newtonianos, a pesar de que el universo en expansión es un modelo que sólo tiene sentido dentro de un marco puramente relativista aunque las ecuaciones que se obtienen de la solución directa de las ecuaciones de campo de Einstein sean idénticas a las que aquí hemos obtenido (ver Tipler 1996 para detalles con respecto a por qué funcionan los argumentos newtonianos).

 índice principal de Cosmología

Copyright 1996-2004 Pedro J. Hernández